题目内容
13.已知二次函数f(x)=ax2+bx-3在x=1处取得极值,且在(0,-3)点处的切线与直线2x+y=0平行.(1)求f(x)的解析式;
(2)求函数g(x)=xf(x)+4x的单调递增区间及极值.
分析 (1)求得函数的导数,由切线方程和极值点,可得f′(0)=-2,f′(1)=0,解方程可得a=1,b=-2,即有函数f(x)的解析式;
(2)求出函数g(x)的导数,求得g(x)的单调区间,即可得到极值.
解答 解:(1)由f(x)=ax2+bx-3,可得f′(x)=2ax+b,
由题设可得$\left\{\begin{array}{l}{f′(0)=-2}\\{f′(1)=0}\end{array}\right.$,即$\left\{\begin{array}{l}{2a+b=0}\\{b=-2}\end{array}\right.$,
解得a=1,b=-2.所以f(x)=x2-2x-3.
(2)由题意得g(x)=xf(x)=x3-2x2+x,
所以g′(x)=3x2-4x+1=(3x-1)(x-1).令g′(x)=0,得${x_1}=\frac{1}{3}$,x2=1.
| x | (-∞,$\frac{1}{3}$) | $\frac{1}{3}$ | ($\frac{1}{3}$,1) | 1 | (1,+∞) |
| g′(x) | + | 0 | - | 0 | + |
| g(x) | 增 | $\frac{4}{27}$ | 减 | 0 | 增 |
在x=1有极小值为0,在x=$\frac{1}{3}$有极大值$\frac{4}{27}$.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值,主要考查导数的几何意义,正确求导和解二次不等式是解题的关键.

练习册系列答案
相关题目
4.满足条件|z-i|=|z+3+4i|的复数z在复平面内对应的点的轨迹是( )
| A. | 一条直线 | B. | 两条直线 | C. | 圆 | D. | 椭圆 |
1.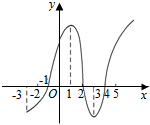 如图所示是y=f(x)的导数图象,则正确的判断是( )
如图所示是y=f(x)的导数图象,则正确的判断是( )
①f(x)在(-3,1)上是增函数;②x=-1是f(x)的极小值点;
③f(x)在(2,4)上是减函数,在(-1,2)上是增函数;④x=2是f(x)的极小值点.
 如图所示是y=f(x)的导数图象,则正确的判断是( )
如图所示是y=f(x)的导数图象,则正确的判断是( )①f(x)在(-3,1)上是增函数;②x=-1是f(x)的极小值点;
③f(x)在(2,4)上是减函数,在(-1,2)上是增函数;④x=2是f(x)的极小值点.
| A. | ①②③ | B. | ②③ | C. | ③④ | D. | ①③④ |
8.曲线$y=\frac{x}{x-2}$在点(1,-1)处的切线方程是( )
| A. | y=2x+1 | B. | y=2x-1 | C. | y=-2x+1 | D. | y=-2x-2 |