题目内容
8.曲线$y=\frac{x}{x-2}$在点(1,-1)处的切线方程是( )| A. | y=2x+1 | B. | y=2x-1 | C. | y=-2x+1 | D. | y=-2x-2 |
分析 求出导数,求得切线的斜率,再由点斜式方程,即可得到切线方程.
解答 解:$y=\frac{x}{x-2}$的导数为y′=-$\frac{2}{(x-2)^{2}}$,
即有曲线在x=1处的切线的斜率为-2,
曲线在x=1处的切线的方程为y+1=-2(x-1),
即为y=-2x+1.
故选:C.
点评 本题考查导数的运用:求切线的斜率,主要考查导数的几何意义,正确求得导数和运用直线的点斜式方程是解题的关键.

练习册系列答案
相关题目
16.下列推理正确的是( )
| A. | 把a(b+c)与 loga(x+y)类比,则有:loga(x+y)=logax+logay | |
| B. | 把a(b+c)与 sin(x+y)类比,则有:sin(x+y)=sinx+siny | |
| C. | 把(ab)n与 (a+b)n类比,则有:(x+y)n=xn+yn. | |
| D. | 把(a+b)+c与 (xy)z类比,则有:(xy)z=x(yz) |
3.若函数f(x)=sin(ωx+θ)的图象(部分)如图所示,则ω和θ的取值是( )
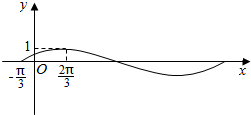

| A. | $ω=1,θ=\frac{π}{3}$ | B. | $ω=1,θ=-\frac{π}{3}$ | C. | $ω=\frac{1}{2},θ=\frac{π}{6}$ | D. | $ω=\frac{1}{2},θ=-\frac{π}{6}$ |