题目内容
选修41:几何证明选讲
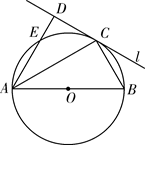
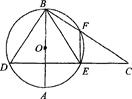
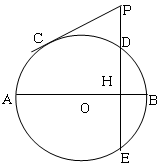
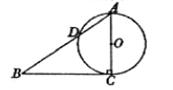
如图,圆O的直径AB=4,C为圆周上一点,BC=2,过C作圆O的切线l,过A作l的垂线AD,AD分别与直线l、圆O交于点D、E,求线段AE的长.

如图,圆O的直径AB=4,C为圆周上一点,BC=2,过C作圆O的切线l,过A作l的垂线AD,AD分别与直线l、圆O交于点D、E,求线段AE的长.
AE=AO=AB=2.
本试题主要是考查了平面几何证明的运用。利用圆的切线的性质和三角形角的关系得到线段的长度的求解。
在Rt△ABC中,因为AB=4,BC=2,所以∠ABC=60°,
因为l为过C的切线,所以∠DCA=∠CBA,
所以∠DCA=∠ABC=60°.………………………………5分
又因为AD⊥DC,所以∠DAC=30°.
在△AOE中,因为∠EAO=∠DAC+∠CAB=60°,且OE=OA,
所以AE=AO=AB=2.…………………………………10分
在Rt△ABC中,因为AB=4,BC=2,所以∠ABC=60°,
因为l为过C的切线,所以∠DCA=∠CBA,
所以∠DCA=∠ABC=60°.………………………………5分
又因为AD⊥DC,所以∠DAC=30°.
在△AOE中,因为∠EAO=∠DAC+∠CAB=60°,且OE=OA,
所以AE=AO=AB=2.…………………………………10分

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 的角平分线AD的延长线交它的外接圆于点E
的角平分线AD的延长线交它的外接圆于点E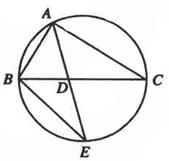
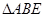
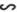
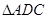
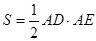 ,求
,求 的大小。
的大小。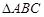 内接于⊙
内接于⊙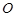 ,
, 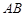 是⊙
是⊙ 是过点
是过点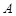 的直线, 且
的直线, 且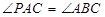 .
.
 交
交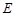 ,
,  ,
,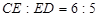 ,
,  , 求
, 求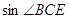 .
.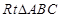 中,
中,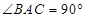 ,
,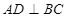 ,
,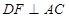 ,垂足为F,
,垂足为F,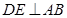 ,垂足为E.
,垂足为E.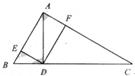
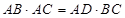 ;
;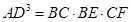
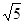 ,求PD的长.
,求PD的长.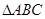 ,过顶点A的圆与边BC切于BC的中点P,与边AB、AC分别交于点M、N,且CN=2BM,点N平分AC.则
,过顶点A的圆与边BC切于BC的中点P,与边AB、AC分别交于点M、N,且CN=2BM,点N平分AC.则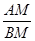 =( )
=( )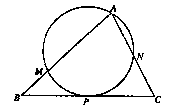
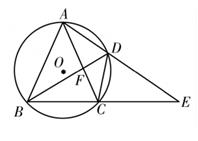
 的内接四边形,延长BC,AD交于点E,且CE=AB=AC,连接BD,交AC于点F.
的内接四边形,延长BC,AD交于点E,且CE=AB=AC,连接BD,交AC于点F. ;
;
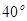 ,则∠DEB___________
,则∠DEB___________