题目内容
16.函数f(x)=3+$\frac{sinx}{{x}^{4}+{x}^{2}+1}$的最大值为M,最小值为m,则M+m=6.分析 令g(x)=$\frac{sinx}{{x}^{4}+{x}^{2}+1}$,由奇偶性的定义可得g(x)为奇函数,设g(x)的最大值为t,最小值即为-t,则f(x)的最大值为M=3+t,最小值为m=3-t,可得M+m=6.
解答 解:函数f(x)=3+$\frac{sinx}{{x}^{4}+{x}^{2}+1}$,
令g(x)=$\frac{sinx}{{x}^{4}+{x}^{2}+1}$,即有g(-x)=$\frac{sin(-x)}{(-x)^{4}+(-x)^{2}+1}$
=-$\frac{sinx}{{x}^{4}+{x}^{2}+1}$=-g(x),
即g(x)为奇函数,
设g(x)的最大值为t,最小值即为-t,
则f(x)的最大值为M=3+t,最小值为m=3-t,
即有M+m=6.
故答案为:6.
点评 本题考查函数的奇偶性的判断和运用:求最值,考查运算能力,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
7.如图所示,程序框图输出的结果为( )
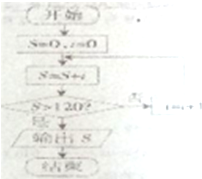

| A. | 15 | B. | 16 | C. | 136 | D. | 153 |
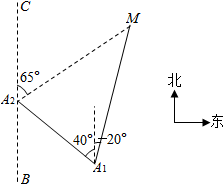 如图,一艘轮船按照北偏西40°的方向以30海里每小时的速度航行,一个灯塔原来在轮船的北偏东20°方向上,经过40分钟后,灯塔在轮船的北偏东65°方向上,则灯塔和轮船原来的距离为10($\sqrt{3}$+1)海里.
如图,一艘轮船按照北偏西40°的方向以30海里每小时的速度航行,一个灯塔原来在轮船的北偏东20°方向上,经过40分钟后,灯塔在轮船的北偏东65°方向上,则灯塔和轮船原来的距离为10($\sqrt{3}$+1)海里.