题目内容
8.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的两条渐进线的斜率之积为-3,左右两支上分别由动点A和B.(1)设直线AB的斜率为1,经过点D(0,5a),且$\overrightarrow{AD}=λ\overrightarrow{DB}$,求实数λ的值.
(2)设点A关于x轴的对称点为M.若直线AB,MB分别与x轴相交于点P,Q,O为坐标原点,证明|OP|•|OQ|=a2.
分析 (1)求得AB的方程,双曲线的渐近线方程,联立直线和双曲线的方程,解方程可得A,B的横坐标,由向量共线的坐标表示,可得实数λ的值;
(2)设A(m,n),B(s,t),M(m,-n),P(p,0),Q(q,0),由三点共线的条件:斜率相等,可得p,q,再由A,B在双曲线上,满足方程,代入|OP|•|OQ|,化简整理即可得证.
解答 解:(1)设直线AB的方程为y=x+5a,
由渐近线方程为y=±$\frac{b}{a}$x,
可得b2=3a2,
双曲线的方程为3x2-y2=3a2,
代入渐近线方程可得,x2-5ax-14a2=0,
解得x=7a或-2a,
即有A的横坐标为-2a,B的横坐标为7a,
则λ=$\frac{0-(-2a)}{7a-0}$=$\frac{2}{7}$;
(2)证明:设A(m,n),B(s,t),M(m,-n),
P(p,0),Q(q,0),
由A,B,P三点共线可得,$\frac{n-t}{m-s}$=$\frac{-t}{p-s}$,
即有p=$\frac{ns-mt}{n-t}$;
由B,M,Q共线可得,$\frac{t+n}{s-m}$=$\frac{-t}{q-s}$,
即有q=$\frac{mt+ns}{n+t}$,
则有|OP|•|OQ|=|$\frac{ns-mt}{n-t}$•$\frac{mt+ns}{n+t}$|
=|$\frac{{n}^{2}{s}^{2}-{m}^{2}{t}^{2}}{{n}^{2}-{t}^{2}}$|,
由A,B在双曲线上,可得m2=a2+$\frac{1}{3}$n2,s2=a2+$\frac{1}{3}$t2,
代入上式,可得|$\frac{{n}^{2}{a}^{2}-{t}^{2}{a}^{2}}{{n}^{2}-{t}^{2}}$|=a2.
故|OP|•|OQ|=a2.
点评 本题考查双曲线的方程和性质,考查渐近线方程的运用,同时考查直线方程和三点共线的条件:斜率相等,考查运算能力,属于中档题.

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案| A. | f(x)=-2cos x | B. | f(x)=2cos x | ||
| C. | f(x)=$\frac{\sqrt{2}}{2}$sin 2x | D. | f(x)=$\frac{\sqrt{2}}{2}$(sin 2x+cos 2x) |
| A. | |x-a|≤3a | B. | |x-a|<3a | C. | |x-a|<0.03a | D. | |x-a|≤0.03a |
| A. | (-∞,-5)∪[-4,+∞) | B. | (-5,-4] | C. | (-∞,-4] | D. | [-4,0) |
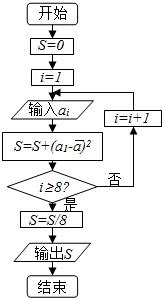 对一名学生数学成绩统计了8次,第i次统计得到的数据为ai,具体如下表所示:
对一名学生数学成绩统计了8次,第i次统计得到的数据为ai,具体如下表所示:| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ai | 100 | 101 | 103 | 103 | 104 | 106 | 107 | 108 |
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
| A. | 椭圆 | B. | 线段 | C. | 双曲线 | D. | 两条射线 |
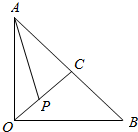 如图,△AOB为等腰直角三角形,OA=1,OC为斜边AB的高,点P在射线OC上,则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为$-\frac{1}{8}$.
如图,△AOB为等腰直角三角形,OA=1,OC为斜边AB的高,点P在射线OC上,则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为$-\frac{1}{8}$.