题目内容
奇函数f(x)满足对任意x∈R都有f(2+x)+f(2-x)=0,且f(1)=9,则f(2010)+f(2011)+f(2012)的值为__________.
—9
解:∵f(2+x)+f(2-x)=0
∴f(2+x)=-f(2-x)
∵f(x)为奇函数
∴f(2+x)=f(x-2);f(0)=0
∴f(x)是以T=4为周期的函数
∵2010=4×502+2;2011=4×503-1;2012=4×503
∵(2+x)+f(2-x)=0
令x=0得f(2)=0
∴f(2010)+f(2011)+f(2012)=f(2)+f(-1)+f(0)=-9
故答案为:-9
∴f(2+x)=-f(2-x)
∵f(x)为奇函数
∴f(2+x)=f(x-2);f(0)=0
∴f(x)是以T=4为周期的函数
∵2010=4×502+2;2011=4×503-1;2012=4×503
∵(2+x)+f(2-x)=0
令x=0得f(2)=0
∴f(2010)+f(2011)+f(2012)=f(2)+f(-1)+f(0)=-9
故答案为:-9

练习册系列答案
相关题目
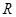 上的偶函数
上的偶函数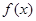 满足
满足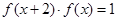 对于
对于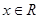 恒成立,且
恒成立,且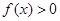 ,则
,则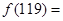 ___▲___.
___▲___.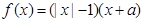 为奇函数,则
为奇函数,则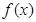 增区间为 .
增区间为 . 是偶函数,当
是偶函数,当 时,
时, ,且当
,且当 时,
时, 恒成立,则
恒成立,则 的最小值是( )
的最小值是( )


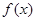 ,有下述命题:
,有下述命题: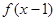 的图象关于点A(1,0)对称;
的图象关于点A(1,0)对称;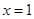 对称,则
对称,则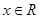 ,有
,有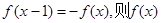 的周期为2;
的周期为2;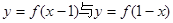 的图象关于直线
的图象关于直线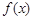 对任意
对任意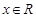 ,都有
,都有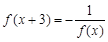 ,且当
,且当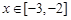 时,
时,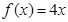 , 则
, 则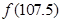 = ( )
= ( ) 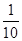
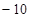
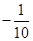
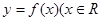 )是奇函数,则下列坐标表示的点一定在函数
)是奇函数,则下列坐标表示的点一定在函数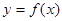 图象上的是
图象上的是 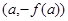
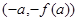
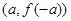
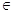 R,则下列各式成立的是
R,则下列各式成立的是 且
且 ,则
,则 ( )
( )

