题目内容
【题目】已知函数f(x)=|x+1|.
(1)若不等式f(x)≥|2x+1|1的解集为A,且![]() ,求实数t的取值范围;
,求实数t的取值范围;
(2)在(1)的条件下,若![]() ,证明:f(ab)>f(a)f(b).
,证明:f(ab)>f(a)f(b).
【答案】(1)(![]() ,2] (2)详见解析
,2] (2)详见解析
【解析】
(1)零点分区间去掉绝对值,得到解集为{x|-1≤x≤1},由集合间的包含关系得到-1≤1-t<t-2≤1,解得![]() ;(2)原式等价于|ab+1|>|a+b|,即证|ab+1|2>|a+b|2,两边展开,提公因式即可得证.
;(2)原式等价于|ab+1|>|a+b|,即证|ab+1|2>|a+b|2,两边展开,提公因式即可得证.
(1)不等式f(x)≥|2x+1|-1,即|x+1|-|2x+1|+1≥0.
当x<-1时,不等式可化为-x-1+(2x+1)+1≥0,解得x≥-1,这时原不等式无解;
当![]() ,不等式可化为x+1+(2x+1)+1≥0,解得x≥-1,这时不等式的解为
,不等式可化为x+1+(2x+1)+1≥0,解得x≥-1,这时不等式的解为![]() ;
;
当![]() 时,不等式可化为x+1-(2x+1)+1≥0,解得x≤1,这时不等式的解为
时,不等式可化为x+1-(2x+1)+1≥0,解得x≤1,这时不等式的解为![]() .
.
所以不等式f(x)≥|2x+1|-1的解集为{x|-1≤x≤1}.
因为[1-t,t-2]![]() A,
A,
所以-1≤1-t<t-2≤1,解得![]() .
.
即实数t的取值范围是(![]() ,2].
,2].
(2)证明:因为f(a)-f(b)=|a+1|-|-b+1|≤a+1-(-b+1)=|a+b|,
所以要证f(ab)>f(a)-f(-b)成立,
只需证|ab+1|>|a+b|,即证|ab+1|2>|a+b|2,
也就是证明a2b2+2ab+1>a2+2ab+b2成立,
即证a2b2-a2-b2+1>0,即证(a2-1)(b2-1)>0.
因为A={x|-1≤x≤1},![]() ,
,
所以|a|>1,|b|>1,a2>1,b2>1.
所以(a2-1)(b2-1)>0成立.
从而对于任意的![]() ,都有f(ab)>f(a)-f(-b)成立.
,都有f(ab)>f(a)-f(-b)成立.

【题目】2020年寒假,因为“新冠”疫情全体学生只能在家进行网上学习,为了研究学生网上学习的情况,某学校随机抽取![]() 名学生对线上教学进行调查,其中男生与女生的人数之比为
名学生对线上教学进行调查,其中男生与女生的人数之比为![]() ,抽取的学生中男生有
,抽取的学生中男生有![]() 人对线上教学满意,女生中有
人对线上教学满意,女生中有![]() 名表示对线上教学不满意.
名表示对线上教学不满意.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对线上教学是否满意 与性别有关”;
的把握认为“对线上教学是否满意 与性别有关”;
态度 性别 | 满意 | 不满意 | 合计 |
男生 | |||
女生 | |||
合计 | 100 |
(2)从被调查的对线上教学满意的学生中,利用分层抽样抽取![]() 名学生,再在这
名学生,再在这![]() 名学生中抽取
名学生中抽取![]() 名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
附: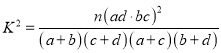 .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下的对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求y关于x的线性回归方程.
(3)如果广告费支出为一千万元,预测销售额大约为多少百万元?
参考公式用最小二乘法求线性回归方程系数公式: ,
,![]() .
.