题目内容
已知y=f(x)满足f(n-1)=f(n)-lg an-1(n≥2,n∈N)且f(1)=-lg a,是否存在实数α,β,使f(n)=(αn2+βn-1)·lg a对任何n∈N*都成立,证明你的结论
∵f(n)=f(n-1)+lg an-1,
令n=2,则f(2)=f(1)+lg a=-lg a+lg a=0.
又f(1)=-lg a,
∴,∴.
∴f(n)=lg a.
现证明如下:(1)当n=1时,显然成立.
(2)假设n=k(k∈N*,且k≥1)时成立,
即f(k)=lg a,
则n=k+1时,
f(k+1)=f(k)+lg ak=f(k)+klg a
=lg a
=lg a.
则当n=k+1时,等式成立.
综合(1)(2)可知,存在实数α、β且α=,β=-,使
f(n)=(αn2+βn-1)lg a对任意n∈N+都成立
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

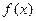 的定义域;
的定义域;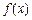 在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数
在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数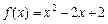 在[1,2]上是否具有“DK”性质,说明理由;
在[1,2]上是否具有“DK”性质,说明理由;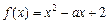 在[a,a+1]上具有“DK”性质,求a的取值范围.
在[a,a+1]上具有“DK”性质,求a的取值范围.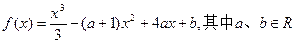
 在
在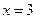 处取得极小值是
处取得极小值是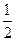 ,求
,求 的值;
的值; 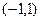 上有且只有一个极值点, 求实数
上有且只有一个极值点, 求实数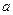 的取值范围.
的取值范围.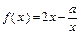 的定义域为(0,1](
的定义域为(0,1](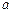 为实数).
为实数).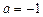 时,求函数
时,求函数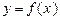 的值域;
的值域;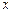 的值
的值 R,m,n都是不为1的正数,函数
R,m,n都是不为1的正数,函数
 ,请判断函数
,请判断函数 是否具有奇偶性. 如果具有,求出相
是否具有奇偶性. 如果具有,求出相 ,且
,且 ,请判断函数
,请判断函数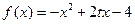 在闭区间
在闭区间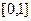 上的最大值记为
上的最大值记为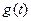
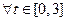 ,
, 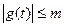 恒成立,求
恒成立,求 的取值范围.
的取值范围.