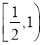题目内容
18.据媒体报道:某市4月份空气质量优良,高居全国榜首,青春中学九年级课外兴趣小组据此提出了“今年究竟能有多少天空气质量达到优良”的问题,他们根据国家环保总局所公布的空气质量级别表(见表1)以及市环保监测站提供的资料,从中随机抽取了今年1~4月份中30天空气综合污染指数,统计数据如下:表1:空气质量级别表
| 空气污染指数 | 0~50 | 51~100 | 101~150 | 151~200 | 201~250 | 251~300 | 大于300 |
| 空气质量级别 | Ⅰ级(优) | Ⅱ级(良) | Ⅲ1(轻微污染) | Ⅲ2(轻度污染) | Ⅳ1(中度污染) | Ⅳ2(中度重污染) | Ⅴ(重度污染) |
30,32,40,42,45,45,77,83,85,87,90,113,127,153,167,
38,45,48,53,57,64,66,77,92,98,130,184,201,235,243.
请根据空气质量级别表和抽查的空气综合污染指数,解答以下问题:
(1)填写频率分布表中未完成的空格;
| 分组 | 频数统计 | 频数 | 频率 |
| 0~50 | 0.30 | ||
| 51~100 | 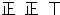 | 12 | 0.40 |
| 101~150 | |||
| 151~200 | 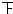 | 3 | 0.10 |
| 201~250 | 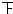 | 3 | 0.10 |
| 合计 | 30 | 30 | 1.00 |
(3)请根据抽样数据,估计该市今年(按360天计算)空气质量是优良(包括Ⅰ、Ⅱ级)的天数.
分析 (1)根据数据进行填表即可;
(2)根据中位数和众数的定义进行求解.
(3)根据空气质量优良的频率和频数进行求解.
解答 (1)
| 分组 | 频数统计 | 频数 | 频率 |
| 0~50 | 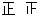 | 9 | 0.30 |
| 51~100 | 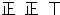 | 12 | 0.40 |
| 101~150 | 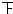 | 3 | 0.10 |
| 151~200 | 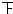 | 3 | 0.10 |
| 201~250 |  | 3 | 0.10 |
| 合计 | 30 | 30 | 1.00 |
(3)∵360×$\frac{9+12}{30}$=252,
∴空气质量优良(包括Ⅰ、Ⅱ级)的天数是252天.
点评 本题主要考查统计的应用,根据数据结合众数,中位数以及频率,频数的概念是解决本题的关键.

练习册系列答案
相关题目
10.已知随机变量X服从正态分布N(1,σ2),且P(-2≤X≤1)=0.4,则P(X>4)=( )
| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.6 |
7.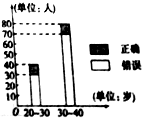 “开门大吉”是某电视台推出的游戏节目,选手面对1-8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,在一次场外调查中,发现参赛选手多数分为两个年龄段:20-30;30-40(单位:岁),其猜对歌曲名称与否的人数如图所示.
“开门大吉”是某电视台推出的游戏节目,选手面对1-8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,在一次场外调查中,发现参赛选手多数分为两个年龄段:20-30;30-40(单位:岁),其猜对歌曲名称与否的人数如图所示.
(1)填写下面2×2列联表:判断是否有90%的把握认为猜对歌曲名称是否与年龄有关,说明你的理由:(下面的临界值表供参考)
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
(2)现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手,并抽取3名幸运选手,求3名幸运选手中至少有一人在20-30岁之间的概率.(已知从6人中取3人的结果有20种)
 “开门大吉”是某电视台推出的游戏节目,选手面对1-8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,在一次场外调查中,发现参赛选手多数分为两个年龄段:20-30;30-40(单位:岁),其猜对歌曲名称与否的人数如图所示.
“开门大吉”是某电视台推出的游戏节目,选手面对1-8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,在一次场外调查中,发现参赛选手多数分为两个年龄段:20-30;30-40(单位:岁),其猜对歌曲名称与否的人数如图所示.(1)填写下面2×2列联表:判断是否有90%的把握认为猜对歌曲名称是否与年龄有关,说明你的理由:(下面的临界值表供参考)
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| 年龄/正误 | 正确 | 错误 | 合计 |
| 20-30 | |||
| 30-40 | |||
| 合计 |
13.已知△ABC的三条边长分别为3,4,5,如果把三角形的三边都增加相同的长度,则这个新三角形的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 由增加的长度决定 |
17.以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,已知圆C的参数方程是$\left\{\begin{array}{l}{x=cosθ-1}\\{y=sinθ-1}\end{array}\right.$(θ为参数),直线l的极坐标方程是ρcosθ+ρsinθ=2,则圆C上的点到直线l的最短距离为( )
| A. | 2$\sqrt{2}$-1 | B. | 2$\sqrt{2}$+1 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
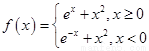 ,若
,若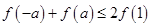 ,则实数
,则实数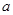 取值范围是( )
取值范围是( )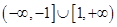 B.
B.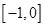
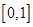 D.
D.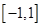
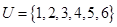 ,集合
,集合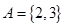 ,集合
,集合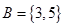 ,则
,则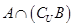 =( )
=( )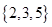 B.
B. C.
C.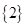 D.
D.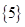
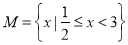 ,函数
,函数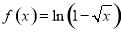 的定义域为
的定义域为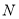 ,则
,则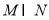 为( )
为( )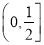 B.
B.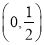 C.
C. D.
D.