题目内容
如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面成锐角α,点B1在底面上的射影D落在BC边上.(1)求证:AC⊥平面BB1C1C;
(2)当α为何值时,AB1⊥BC1,且使D点恰为BC的中点?并说明理由;
(3)当AB1⊥BC1,且D为BC中点时,若BC=2,四棱锥A-BB1C1C的体积为![]() ,求二面角A-B1C1-C的大小.
,求二面角A-B1C1-C的大小.
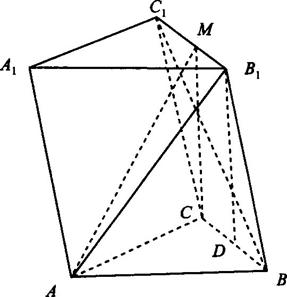
第19题图
答案:(1)∵B1D⊥平面ACB,∴B1D⊥AC,
∵AC⊥BC,∴AC⊥平面BB1C1C.
(2)因为AC⊥平面BB1C1C,所以要使AB1⊥BC1,只要BC1⊥B1C,又BB1C1C是平行四边形,只要BB1C1C是菱形,另外要使D为BC中点,因B1D⊥BC,所以只要三角形B1BC为等边三角形即可,即当α=60°时满足题目要求.
(3)取B1C1的中点M,连接AM、MC,如图所示.因为△C1B1C是等边三角形,所以CM⊥B1C1,

第19题图
由题意知∠AMC是二面角A-B1C1-C的平面角,因为四棱锥A-BB1C1C的体积为![]() ,
,
所以,![]() ·AC·BC·B1D=
·AC·BC·B1D=![]() ,即
,即![]() ×AC×2×
×AC×2×![]() =
=![]() AC=1,
AC=1,
∴tan∠AMC=![]() ∠AMC=30°
∠AMC=30°
即二面角A-B1C1-C的大小为30°.

练习册系列答案
相关题目
 (甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=
(甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC= 如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成的角为
如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成的角为 如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为
如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为 (2011•孝感模拟)如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角为θ,且
(2011•孝感模拟)如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角为θ,且 (2012•梅州二模)如图,已知斜三棱柱ABC-A1B1C1中,点B1在底面ABC上的射影落在BC上,CA=CB=a,AB=
(2012•梅州二模)如图,已知斜三棱柱ABC-A1B1C1中,点B1在底面ABC上的射影落在BC上,CA=CB=a,AB=