题目内容
(不计入总分):已知函数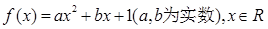 ,设函数
,设函数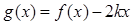 ,
,
(3)当a≠0时,求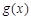 在
在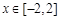 上的最小值
上的最小值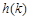 .
.
(3) 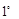 当
当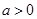 时,①当
时,①当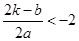 ,即
,即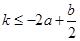 时,
时, 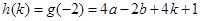
②当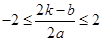 ,即
,即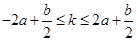 时,
时, 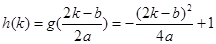
③当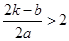 ,即
,即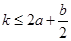 时,
时, 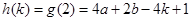
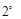 当
当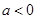 时, ①当
时, ①当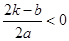 ,即
,即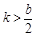 时,
时, 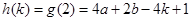
②当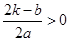 ,即
,即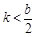 时,
时, 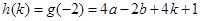
解析

练习册系列答案
相关题目
题目内容
(不计入总分):已知函数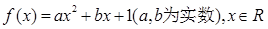 ,设函数
,设函数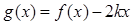 ,
,
(3)当a≠0时,求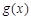 在
在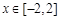 上的最小值
上的最小值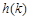 .
.
(3) 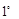 当
当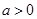 时,①当
时,①当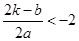 ,即
,即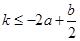 时,
时, 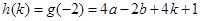
②当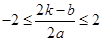 ,即
,即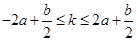 时,
时, 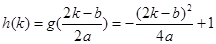
③当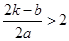 ,即
,即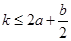 时,
时, 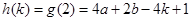
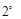 当
当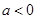 时, ①当
时, ①当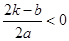 ,即
,即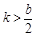 时,
时, 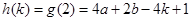
②当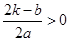 ,即
,即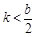 时,
时, 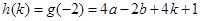
解析
