题目内容
函数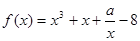
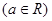 在区间
在区间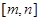 上有最大值10,则函数
上有最大值10,则函数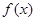 在区间
在区间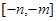 上有
上有
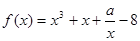
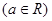 在区间
在区间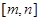 上有最大值10,则函数
上有最大值10,则函数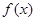 在区间
在区间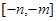 上有
上有| A.最大值-10 | B.最小值-10 | C.最小值-26 | D.最大值-26 |
C
可以令g(x)=x3+x+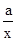 ,因为函数f(x)=x3+x+
,因为函数f(x)=x3+x+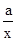 -8(a∈R)在区间[m,n]上有最大值10,说明g(x)的最大值为18,再根据奇函数的性质进行求解;
-8(a∈R)在区间[m,n]上有最大值10,说明g(x)的最大值为18,再根据奇函数的性质进行求解;
解答:解:∵函数f(x)=x3+x+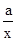 -8(a∈R)在区间[m,n]上有最大值10,
-8(a∈R)在区间[m,n]上有最大值10,
∴令g(x)=x3+x+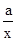 ,可得g(x)在区间[m,n]上又最大值为18,
,可得g(x)在区间[m,n]上又最大值为18,
因为g(-x)=(-x)3-x-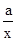 =-(x3+x+
=-(x3+x+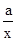 )=-g(x),
)=-g(x),
∴g(x)是奇函数,
∴g(x)在区间[-n,-m]上有最小值为-18,
∴函数f(x)=x3+x+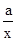 -8(a∈R)的最小值为-18-8=-26,
-8(a∈R)的最小值为-18-8=-26,
故选C;
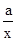 ,因为函数f(x)=x3+x+
,因为函数f(x)=x3+x+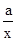 -8(a∈R)在区间[m,n]上有最大值10,说明g(x)的最大值为18,再根据奇函数的性质进行求解;
-8(a∈R)在区间[m,n]上有最大值10,说明g(x)的最大值为18,再根据奇函数的性质进行求解;解答:解:∵函数f(x)=x3+x+
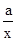 -8(a∈R)在区间[m,n]上有最大值10,
-8(a∈R)在区间[m,n]上有最大值10,∴令g(x)=x3+x+
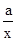 ,可得g(x)在区间[m,n]上又最大值为18,
,可得g(x)在区间[m,n]上又最大值为18,因为g(-x)=(-x)3-x-
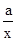 =-(x3+x+
=-(x3+x+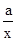 )=-g(x),
)=-g(x),∴g(x)是奇函数,
∴g(x)在区间[-n,-m]上有最小值为-18,
∴函数f(x)=x3+x+
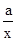 -8(a∈R)的最小值为-18-8=-26,
-8(a∈R)的最小值为-18-8=-26,故选C;

练习册系列答案
相关题目
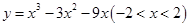 有 ( ).
有 ( ).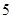 ,极小值
,极小值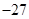 ;
;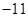 ;
;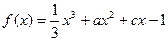 在区间(1,2)单调递减。
在区间(1,2)单调递减。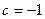 时,求a的取值范围;
时,求a的取值范围;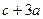 的取值范围。
的取值范围。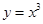 的递减区间为( )
的递减区间为( )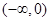
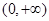
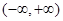
 图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,导数f/(x)的 最小值为-12,求a,b,c的值.
图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,导数f/(x)的 最小值为-12,求a,b,c的值.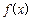 的导函数
的导函数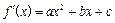 的图象如右图,
的图象如右图,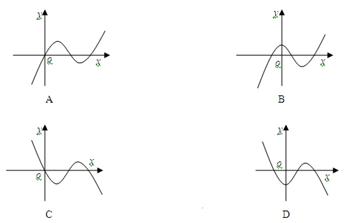
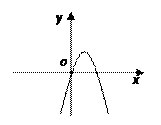
 在
在 处取得极值,则
处取得极值,则 。
。