题目内容
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,且满足
上,且满足![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过抛物线![]() 上的任意一点
上的任意一点![]() 作抛物线
作抛物线![]() 的切线,交抛物线
的切线,交抛物线![]() 的准线于点
的准线于点![]() .在
.在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() ,使以
,使以![]() 为直径的圆恒过
为直径的圆恒过![]() .若存在,求出
.若存在,求出![]() 的坐标,若不存在,则说明理由.
的坐标,若不存在,则说明理由.
【答案】(1)![]() (2)存在一个定点
(2)存在一个定点![]() ,使以
,使以![]() 为直径的圆恒过
为直径的圆恒过![]()
【解析】
(1)利用抛物线的定义,结合![]() ,求得
,求得![]() ,由此求得抛物线
,由此求得抛物线![]() 的方程.
的方程.
(2)首先假设存在一个![]() ,使以
,使以![]() 为直径的圆恒过
为直径的圆恒过![]() .设出切线
.设出切线![]() 的方程,利用导数建立切线斜率的等量关系式,结合
的方程,利用导数建立切线斜率的等量关系式,结合![]()
![]() ,利用向量数量积的坐标运算列方程,解方程求得
,利用向量数量积的坐标运算列方程,解方程求得![]() 点的坐标,由此证得存在
点的坐标,由此证得存在![]() 点符合题意.
点符合题意.
(1)由抛物线定义知![]() ,又
,又![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴抛物线![]() 的方程为
的方程为![]() .
.
(2)存在一个![]() ,使以
,使以![]() 为直径的圆恒过
为直径的圆恒过![]() .
.
由(1)得抛物线![]() 为
为![]() ,准线方程为
,准线方程为![]() .
.
依题意切线![]() 斜率一定存在且不为0,设切线
斜率一定存在且不为0,设切线![]() 方程为
方程为![]() .
.
设定点为![]() ,
,![]() ,
,![]() ,
,
∵![]() ,∴切线斜率
,∴切线斜率![]() ,又
,又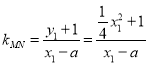 ,
,
∵![]() ,∴
,∴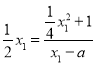 ,解得
,解得![]() .
.
以![]() 为直径的圆恒过定点
为直径的圆恒过定点![]() 等价于
等价于![]() .
.
∴![]() ,
,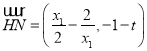 .
.
∴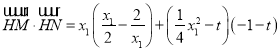
![]() 恒成立.
恒成立.
∴![]() 且
且![]() ,解得
,解得![]() ,存在一个定点
,存在一个定点![]() ,使以
,使以![]() 为直径的圆恒过
为直径的圆恒过![]() .
.

【题目】通过随机询问某地100名高中学生在选择座位时是否挑同桌,得到如下![]() 列联表:
列联表:
男生 | 女生 | 合计 | |
挑同桌 | 30 | 40 | 70 |
不挑同桌 | 20 | 10 | 30 |
总计 | 50 | 50 | 100 |
![]() Ⅰ
Ⅰ![]() 从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
![]() Ⅱ
Ⅱ![]() 根据以上
根据以上![]() 列联表,是否有
列联表,是否有![]() 以上的把握认为“性别与在选择座位时是否挑同桌”有关?
以上的把握认为“性别与在选择座位时是否挑同桌”有关?
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() 参考公式:
参考公式: ![]() ,其中
,其中![]()
【题目】对于定义域为R的函数y=f(x),部分x与y的对应关系如表:
x | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 0 | 2 | 3 | 2 | 0 | ﹣1 | 0 | 2 |
(1)求f{f[f(0)]};
(2)数列{xn}满足x1=2,且对任意n∈N*,点(xn,xn+1)都在函数y=f(x)的图象上,求x1+x2+…+x4n;
(3)若y=f(x)=Asin(ωx+φ)+b,其中A>0,0<ω<π,0<φ<π,0<b<3,求此函数的解析式,并求f(1)+f(2)+…+f(3n)(n∈N*).