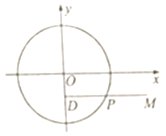
题目内容
【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的x轴的正半轴重合.直线l的参数方程是 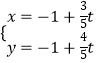 (t为参数),曲线C的极坐标方程为ρ=
(t为参数),曲线C的极坐标方程为ρ= ![]() sin(
sin( ![]() ).
).
(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于M、N两点,求M、N两点间的距离.
【答案】
(1)解:将曲线C的极坐标方程化为ρ= ![]() sin(
sin( ![]() )=cosθ+sinθ
)=cosθ+sinθ
两边都乘以ρ,得ρ2=ρcosθ+ρsinθ
因为x=ρcosθ,y=ρsinθ,ρ2=x2+y 2
代入上式,得方求曲线C的直角坐标方程为:x2+y2﹣x﹣y=0
(2)解:直线l的参数方程是 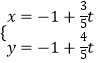 (t为参数),消去参数t得普通方程:4x﹣3y+1=0,将圆C的极坐标方程化为普通方程为:x2+y2﹣x﹣y=0,
(t为参数),消去参数t得普通方程:4x﹣3y+1=0,将圆C的极坐标方程化为普通方程为:x2+y2﹣x﹣y=0,
所以( ![]() )为圆心,半径等于
)为圆心,半径等于 ![]()
所以,圆心C到直线l的距离d= ![]()
所以直线l被圆C截得的弦长为:|MN|=2 ![]() =
= ![]() .
.
即M、N两点间的距离为 ![]()
【解析】(1)利用直角坐标与极坐标间的关系,将曲线C的极坐标方程:ρ=2 ![]() sin(θ+
sin(θ+ ![]() )化成直角坐标方程:x2+y2﹣x﹣y=0,问题得以解决;(2)先将直线l的参数方程化成普通方程:4x﹣3y+1=0,由(1)得曲线C是以(
)化成直角坐标方程:x2+y2﹣x﹣y=0,问题得以解决;(2)先将直线l的参数方程化成普通方程:4x﹣3y+1=0,由(1)得曲线C是以( ![]() )为圆心,半径等于
)为圆心,半径等于 ![]() 的圆,结合点到直线的距离公式及圆的几何性质,可求得M、N两点间的距离.
的圆,结合点到直线的距离公式及圆的几何性质,可求得M、N两点间的距离.
【考点精析】解答此题的关键在于理解直线的参数方程的相关知识,掌握经过点![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 的参数方程可表示为
的参数方程可表示为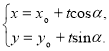 (
(![]() 为参数).
为参数).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目