题目内容
(本小题满分14分)
已知数列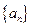 是各项均不为
是各项均不为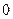 的等差数列,公差为
的等差数列,公差为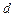 ,
,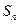 为其前
为其前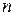 项和,且满足
项和,且满足
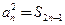 ,
,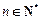 .数列
.数列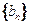 满足
满足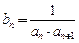 ,
,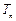 为数列
为数列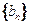 的前n项和.
的前n项和.
(1)求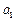 、
、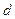 和
和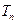 ;
;
(2)若对任意的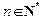 ,不等式
,不等式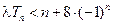 恒成立,求实数
恒成立,求实数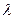 的取值范围;
的取值范围;
(3)是否存在正整数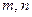
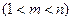 ,使得
,使得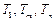 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有
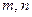 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知数列
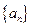 是各项均不为
是各项均不为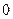 的等差数列,公差为
的等差数列,公差为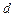 ,
,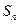 为其前
为其前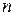 项和,且满足
项和,且满足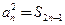 ,
,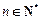 .数列
.数列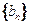 满足
满足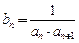 ,
,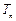 为数列
为数列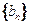 的前n项和.
的前n项和.(1)求
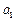 、
、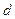 和
和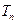 ;
;(2)若对任意的
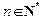 ,不等式
,不等式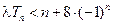 恒成立,求实数
恒成立,求实数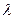 的取值范围;
的取值范围;(3)是否存在正整数
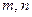
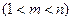 ,使得
,使得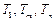 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有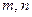 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.解:(1)(法一)在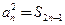 中,令
中,令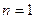 ,
,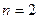 ,
,
得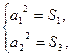 即
即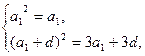 ……………………………………2分
……………………………………2分
解得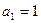 ,
,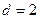 , ………………………………………3分
, ………………………………………3分
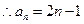 .
.
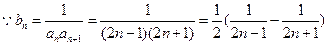 ,
,
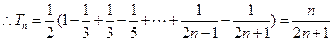 . ……………………5分
. ……………………5分
(法二)
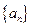 是等差数列,
是等差数列, 
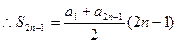
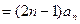 . …………………………2分
. …………………………2分
由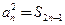 ,得
,得 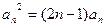 ,
,
又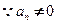 ,
,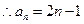 ,则
,则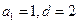 . ………………………3分
. ………………………3分
(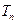 求法同法一)
求法同法一)
(2)①当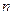 为偶数时,要使不等式
为偶数时,要使不等式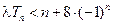 恒成立,即需不等式
恒成立,即需不等式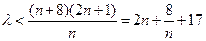 恒成立. …………………………………6分
恒成立. …………………………………6分
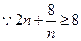 ,等号在
,等号在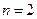 时取得.
时取得.
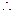 此时
此时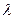 需满足
需满足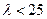 . …………………………………………7分
. …………………………………………7分
②当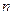 为奇数时,要使不等式
为奇数时,要使不等式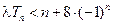 恒成立,即需不等式
恒成立,即需不等式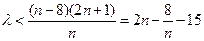 恒成立. …………………………………8分
恒成立. …………………………………8分
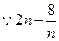 是随
是随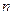 的增大而增大,
的增大而增大, 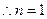 时
时 取得最小值
取得最小值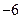 .
.
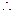 此时
此时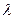 需满足
需满足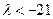 . …………………………………………9分
. …………………………………………9分
综合①、②可得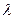 的取值范围是
的取值范围是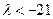 . …………………………………………10分
. …………………………………………10分
(3)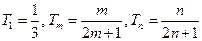 ,
,
若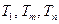 成等比数列,则
成等比数列,则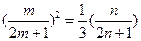 ,即
,即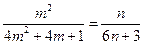 .…11分
.…11分
(法一)由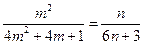 , 可得
, 可得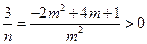 ,
,
即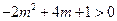 , …………………………………12分
, …………………………………12分
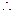
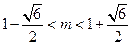 . ……………………………………13分
. ……………………………………13分
又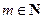 ,且
,且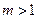 ,所以
,所以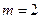 ,此时
,此时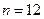 .
.
因此,当且仅当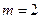 ,
, 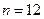 时,
时, 数列
数列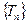 中的
中的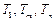 成等比数列.…………14分
成等比数列.…………14分
(法二)因为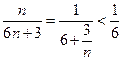 ,故
,故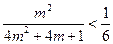 ,即
,即
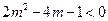 ,
,
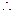
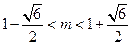 ,(以下同上). …………………………………………13分
,(以下同上). …………………………………………13分
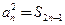 中,令
中,令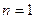 ,
,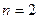 ,
,得
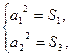 即
即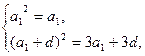 ……………………………………2分
……………………………………2分解得
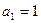 ,
,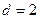 , ………………………………………3分
, ………………………………………3分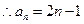 .
.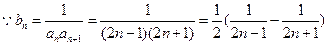 ,
,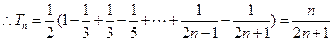 . ……………………5分
. ……………………5分(法二)

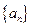 是等差数列,
是等差数列, 
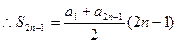
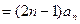 . …………………………2分
. …………………………2分由
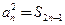 ,得
,得 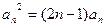 ,
, 又
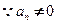 ,
,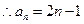 ,则
,则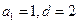 . ………………………3分
. ………………………3分(
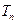 求法同法一)
求法同法一)(2)①当
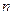 为偶数时,要使不等式
为偶数时,要使不等式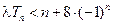 恒成立,即需不等式
恒成立,即需不等式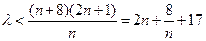 恒成立. …………………………………6分
恒成立. …………………………………6分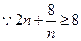 ,等号在
,等号在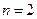 时取得.
时取得. 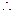 此时
此时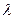 需满足
需满足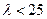 . …………………………………………7分
. …………………………………………7分②当
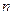 为奇数时,要使不等式
为奇数时,要使不等式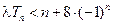 恒成立,即需不等式
恒成立,即需不等式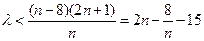 恒成立. …………………………………8分
恒成立. …………………………………8分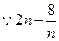 是随
是随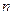 的增大而增大,
的增大而增大, 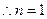 时
时 取得最小值
取得最小值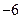 .
. 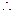 此时
此时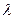 需满足
需满足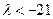 . …………………………………………9分
. …………………………………………9分综合①、②可得
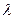 的取值范围是
的取值范围是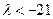 . …………………………………………10分
. …………………………………………10分(3)
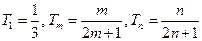 ,
, 若
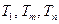 成等比数列,则
成等比数列,则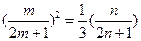 ,即
,即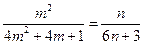 .…11分
.…11分(法一)由
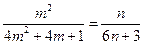 , 可得
, 可得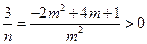 ,
,即
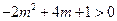 , …………………………………12分
, …………………………………12分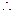
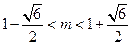 . ……………………………………13分
. ……………………………………13分又
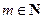 ,且
,且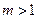 ,所以
,所以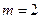 ,此时
,此时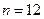 .
.因此,当且仅当
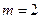 ,
, 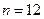 时,
时, 数列
数列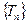 中的
中的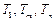 成等比数列.…………14分
成等比数列.…………14分(法二)因为
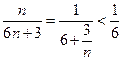 ,故
,故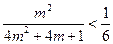 ,即
,即
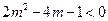 ,
,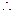
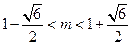 ,(以下同上). …………………………………………13分
,(以下同上). …………………………………………13分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

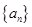 是等差数列且
是等差数列且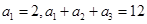 。(1)求数列
。(1)求数列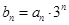 ,求数列
,求数列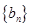 的前
的前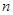 项和
项和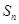 。
。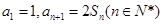 。(1)求数列
。(1)求数列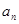 (2)求数列
(2)求数列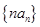 前
前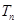 。
。 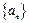 是公差为
是公差为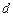 的等差数列,其前
的等差数列,其前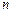 项和为
项和为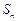 .
.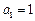 ,
,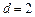 ,
,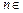
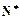 时,
时,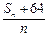 的最小值;
的最小值;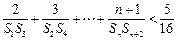 ;
;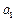 ,使得对任意正整数
,使得对任意正整数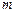 的不等式
的不等式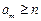 的最小正整数解为
的最小正整数解为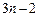 ?若存在,则求
?若存在,则求 满足
满足 且
且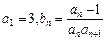 ,数列
,数列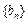 的前
的前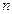 项和为
项和为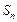 。
。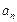 ; (2)求
; (2)求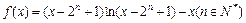 ,求证:
,求证: ≥
≥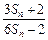 。
。 (
(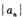 满足,
满足,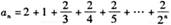 ,则
,则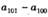 的整数部分为
的整数部分为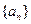 的前20项的和为100,那么
的前20项的和为100,那么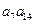 的最大值为( )
的最大值为( )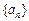 满足
满足 ,且
,且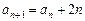 ,
,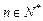 ,那么
,那么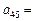 。
。