题目内容

(Ⅰ)
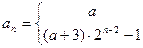
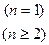
(Ⅱ) 证明略
解:(Ⅰ)由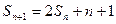 得
得 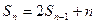
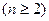
两式相减得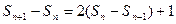 即
即 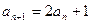
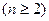
∴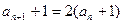 即
即 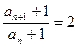
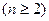 …………(3分)
…………(3分)
故数列{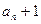 }是从第2项起,以
}是从第2项起,以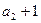 为首项,2为公比的等比数列
为首项,2为公比的等比数列
又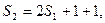
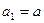 ∴
∴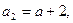 故
故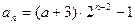
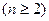
又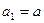 不满足
不满足 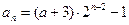
∴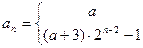
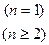 ………(6分)
………(6分)
(Ⅱ) 证明:由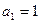 得
得 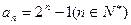 则
则
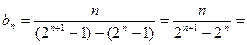
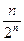 , …………(7分)
, …………(7分)
∴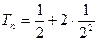 +
+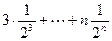 ①
①
从而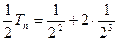 +
+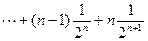 ② ……(9分)
② ……(9分)
①-②得: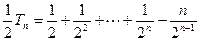 故
故 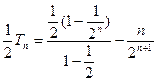 …(11分)
…(11分)
∴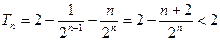 ………(12分)
………(12分)
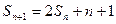 得
得 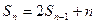
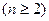
两式相减得
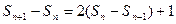 即
即 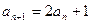
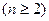
∴
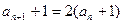 即
即 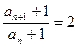
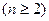 …………(3分)
…………(3分)故数列{
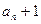 }是从第2项起,以
}是从第2项起,以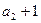 为首项,2为公比的等比数列
为首项,2为公比的等比数列又
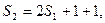
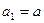 ∴
∴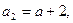 故
故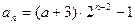
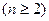
又
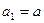 不满足
不满足 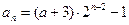
∴
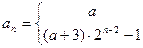
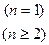 ………(6分)
………(6分)(Ⅱ) 证明:由
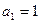 得
得 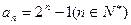 则
则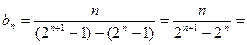
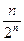 , …………(7分)
, …………(7分)∴
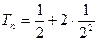 +
+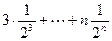 ①
①从而
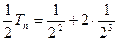 +
+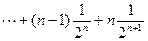 ② ……(9分)
② ……(9分)①-②得:
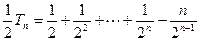 故
故 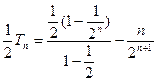 …(11分)
…(11分)∴
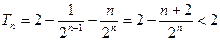 ………(12分)
………(12分)
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
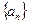 满足:
满足: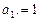 ,
,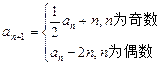
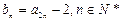 ,求证
,求证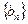 是等比数列,并求其通项公式;
是等比数列,并求其通项公式; )
)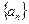 的公差为
的公差为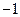 , 且
, 且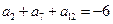 ,
,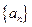 的通项公式
的通项公式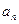 与前
与前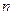 项和
项和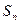 ;
;  项抽去其中一项后,剩下三项按原来顺序恰为等比数列
项抽去其中一项后,剩下三项按原来顺序恰为等比数列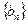
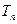 , 若存在
, 若存在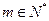 , 使对任意
, 使对任意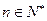 总有
总有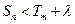 恒成立, 求实数
恒成立, 求实数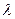 的取值范围.K
的取值范围.K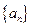 是各项均不为
是各项均不为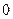 的等差数列,公差为
的等差数列,公差为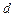 ,
,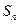 为其前
为其前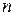 项和,且满足
项和,且满足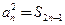 ,
,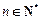 .数列
.数列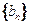 满足
满足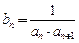 ,
,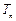 为数列
为数列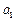 、
、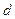 和
和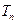 ;
;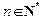 ,不等式
,不等式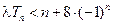 恒成立,求实数
恒成立,求实数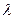 的取值范围;
的取值范围;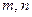
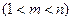 ,使得
,使得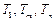 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有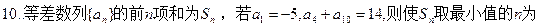
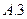
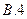

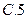
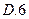
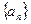 满足
满足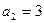 ,
,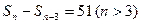 ,
,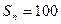 ,则
,则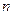 的
的 值为
值为
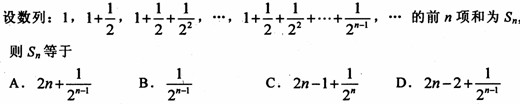
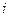 行第
行第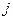 个数表示
个数表示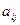 (i
(i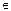 N*,j
N*,j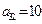 ,若
,若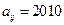 ,则
,则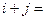 ▲ .
▲ .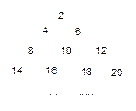

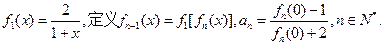
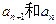 的递推关系式,并求出
的递推关系式,并求出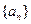 的通项公式;
的通项公式;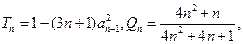 试比较
试比较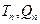 大小
大小 并证明
并证明