题目内容
16.已知a,b∈R,a+b=3,则当然2a+2b取最小值时,ab=$\frac{9}{4}$.分析 由题意和基本不等式可得2a+2b≥2$\sqrt{{2}^{a}•{2}^{b}}$=2$\sqrt{{2}^{a+b}}$=4$\sqrt{2}$,由等号成立的条件可得ab的值.
解答 解:∵a,b∈R,a+b=3,
∴2a+2b≥2$\sqrt{{2}^{a}•{2}^{b}}$=2$\sqrt{{2}^{a+b}}$=4$\sqrt{2}$
当且仅当2a=2b即a=b=$\frac{3}{2}$时,上式取最小值4$\sqrt{2}$,
∴ab=$\frac{9}{4}$
故答案为:$\frac{9}{4}$.
点评 本题考查基本不等式求最值,属基础题.

练习册系列答案
相关题目
7.如图,I表示全集,图中的阴影部分表示的集合是( )
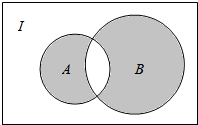

| A. | ∁I(A∩B) | B. | ∁I(A∪B) | C. | (A∩∁IB)∪(B∩∁IA) | D. | (A∪∁IB)∩(B∪∁IA) |
11.在△ABC中,若∠A=90°,BC=2$\sqrt{3}$,O为中线AM上一动点,则$\overrightarrow{OA}•(\overrightarrow{OB}+\overrightarrow{OC})$的最小值是( )
| A. | -$\frac{9}{2}$ | B. | -$\frac{7}{2}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{1}{2}$ |