题目内容
正方体ABCD-A1B1C1D1中,长度为定值的线段EF在线段B1D1上滑动,现有五个命题如下:
①AC⊥BE;
②EF∥平面A1BD;
③直线AE与BF所成角为定值;
④直线AE与平面BD1所成角为定值;
⑤三棱锥A-BEF的体积为定值.
其中正确命题序号为______.
①AC⊥BE;
②EF∥平面A1BD;
③直线AE与BF所成角为定值;
④直线AE与平面BD1所成角为定值;
⑤三棱锥A-BEF的体积为定值.
其中正确命题序号为______.
①正确.如图1所示,连接BD, 由正方体ABCD-A1B1C1D1中可得AC⊥BD,BB1⊥AC,BD∩BB1=B,∴AC⊥平面BDD1B1,∴AC⊥BE;
由正方体ABCD-A1B1C1D1中可得AC⊥BD,BB1⊥AC,BD∩BB1=B,∴AC⊥平面BDD1B1,∴AC⊥BE;
②正确.如图图2所示,∵B1D1∥BD,B1D1?平面A1BD,而BD?平面A1BD,∴EF∥平面A1BD;
③不正确.如图3所示,建立空间直角坐标系,不妨设正方体的棱长为1,|EF|=m,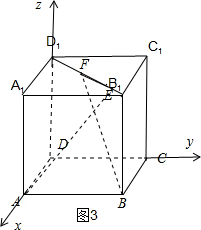 F(a,b,1),
F(a,b,1),
则E(a+
m,b+
m,1).又A(1,0,0),B(1,1,0).
∴
=(a+
m-1,b+
m,1),
=(a-1,b-1,1),
∴cos<
,
>=
=
,与a,b的取值有关系.
④如图3所示,取对角面BD1的法向量为
=(-1,1,0).
设AE与平面BD1所成的角为θ,则sinθ=|cos<
,
>|=
=
与a,b的取值有关系;
⑤正确.由①可知:AC⊥平面BDD1B1,∴点A到平面BEF的距离=
|AC|,而△BEF的面积=
|EF||BB1|,∴VA-BEF=
×
|AC|•
|EF||BB1|,又|AC|,|EF|,|BB1|都为定值,因此三棱锥A-BEF的体积为定值.
综上可知:正确答案为①②⑤.
故答案为①②⑤.
 由正方体ABCD-A1B1C1D1中可得AC⊥BD,BB1⊥AC,BD∩BB1=B,∴AC⊥平面BDD1B1,∴AC⊥BE;
由正方体ABCD-A1B1C1D1中可得AC⊥BD,BB1⊥AC,BD∩BB1=B,∴AC⊥平面BDD1B1,∴AC⊥BE;②正确.如图图2所示,∵B1D1∥BD,B1D1?平面A1BD,而BD?平面A1BD,∴EF∥平面A1BD;

③不正确.如图3所示,建立空间直角坐标系,不妨设正方体的棱长为1,|EF|=m,
 F(a,b,1),
F(a,b,1),则E(a+
| ||
| 2 |
| ||
| 2 |
∴
| AE |
| ||
| 2 |
| ||
| 2 |
| BF |
∴cos<
| AE |
| BF |
| ||||
|
|
(a+
| ||||||||||||
|
④如图3所示,取对角面BD1的法向量为
| AC |
设AE与平面BD1所成的角为θ,则sinθ=|cos<
| AE |
| n |
|
| ||||
|
|
|1-a-
| ||||||||||||
|
⑤正确.由①可知:AC⊥平面BDD1B1,∴点A到平面BEF的距离=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
综上可知:正确答案为①②⑤.
故答案为①②⑤.

练习册系列答案
相关题目