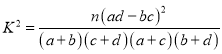题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 过右焦点
过右焦点![]() ,过点
,过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点(均不为顶点)
两点(均不为顶点)
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 是椭圆
是椭圆![]() 的右顶点,直线
的右顶点,直线![]() ,若直线
,若直线![]() 与直线
与直线![]() 交于点
交于点![]() 直线
直线![]() 与直线
与直线![]() 交于点
交于点![]() ,试判断
,试判断![]() 是否为定值,若是,求出定值,若不是请说明理由.
是否为定值,若是,求出定值,若不是请说明理由.
【答案】(1)![]() (2)是定值,定值为0.
(2)是定值,定值为0.
【解析】
(1)由直线![]() 过右焦点
过右焦点![]() ,求得
,求得![]() ,可得
,可得![]() ,由离心率公式可得
,由离心率公式可得![]() ,结合
,结合![]() ,
,![]() ,
,![]() 的关系可得
的关系可得![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(2)求得![]() 的坐标,设出直线
的坐标,设出直线![]() ,设
,设![]() ,
,![]() ,求得
,求得![]() ,
,![]() 的坐标,运用向量的加减和数量积的坐标运算,化简整理,再由直线
的坐标,运用向量的加减和数量积的坐标运算,化简整理,再由直线![]() 和椭圆方程联立,消去
和椭圆方程联立,消去![]() ,可得
,可得![]() 的二次方程,运用韦达定理,计算可得所求定值.
的二次方程,运用韦达定理,计算可得所求定值.
(1)![]() 直线
直线![]() 过右焦点
过右焦点![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
又![]() 椭圆C的离心率为
椭圆C的离心率为![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
则![]() .
.
![]() 椭圆C的方程为
椭圆C的方程为![]()
(2)设![]() 的中点为
的中点为![]() ,
,
则![]() .
.
当![]() 轴时,
轴时,![]() .
.
当![]() 不与
不与![]() 轴垂直时,
轴垂直时,
设直线![]() 的方程为
的方程为![]() .
.
由(1)知![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,![]() ,
,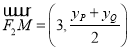 ,
,![]() .
.
易知![]() ,
,![]() ,
,![]() 三点共线,
三点共线,
![]()
![]() ,
,
可得![]() ,
,
解得![]() ;
;
同理,可得![]()
联立直线![]() 与椭圆C的方程,得
与椭圆C的方程,得 ,整理得
,整理得![]() ,
,
![]()
![]() ,
,![]() .
.
则![]()
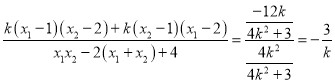 ,
,
![]()
![]() .
.
又![]()
![]() ,
,
![]()
![]()
综上所述,![]() 是定值,定值为
是定值,定值为![]() .
.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】2019年末,武汉出现新型冠状病毒(![]() 肺炎疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,目前没有特异治疗方法.防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,某社区将本社区的排查工作人员分为
肺炎疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,目前没有特异治疗方法.防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,某社区将本社区的排查工作人员分为![]() ,
,![]() 两个小组,排查工作期间社区随机抽取了100户已排查户,进行了对排查工作态度是否满意的电话调查,根据调查结果统计后,得到如下
两个小组,排查工作期间社区随机抽取了100户已排查户,进行了对排查工作态度是否满意的电话调查,根据调查结果统计后,得到如下![]() 的列联表.
的列联表.
是否满意 组别 | 不满意 | 满意 | 合计 |
| 16 | 34 | 50 |
| 2 | 45 | 50 |
合计 | 21 | 79 | 100 |
(1)分别估计社区居民对![]() 组、
组、![]() 组两个排查组的工作态度满意的概率;
组两个排查组的工作态度满意的概率;
(2)根据列联表的数据,能否有![]() 的把握认为“对社区排查工作态度满意”与“排查工作组别”有关?
的把握认为“对社区排查工作态度满意”与“排查工作组别”有关?
附表:
|
|
|
|
|
|
|
|
|
|
|
|
附: