题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)讨论![]() 在区间
在区间![]() 上的零点个数.
上的零点个数.
【答案】(1)![]() .(2)见解析
.(2)见解析
【解析】
(1)求出![]() ,从而可知切线的斜率
,从而可知切线的斜率![]() ,由直线的点斜式可求切线方程.
,由直线的点斜式可求切线方程.
(2)设![]() ,通过导数可探究单调性,再结合
,通过导数可探究单调性,再结合![]() ,
,![]() ,
,![]() ,
,![]() ,可得
,可得![]() 函数图像,通过讨论当
函数图像,通过讨论当![]() 或
或![]() ,当
,当![]() 或
或![]() 或
或![]() ,当
,当![]() 或
或![]() 时,结合函数图像,可求零点个数.
时,结合函数图像,可求零点个数.
解:(1)因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() ,则
,则![]() ,故切线方程为
,故切线方程为![]() .
.
(2)令![]() ,得
,得![]() ,设
,设![]() ,
,
则![]() ,由
,由![]() 恒成立,
恒成立,
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() 或
或![]() ,
,
则![]() 在
在![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
因为![]() ,
, ,
, ,
,
 .则
.则![]() 的简图为
的简图为

当![]() 或
或![]() 时,
时,![]() 无解,即
无解,即![]() 在区间
在区间![]() 上没有零点;
上没有零点;
当![]() 或
或![]() 或
或![]() 时,
时,![]() 在区间
在区间![]() 上有且仅有一个零点;
上有且仅有一个零点;
当![]() 或
或![]() 时,
时,![]() 在区间
在区间![]() 上有两个零点.
上有两个零点.
综上,当![]() 或
或![]() 时,
时,![]() 在区间
在区间![]() 上没有零点;
上没有零点;
当![]() 或
或![]() 或
或![]() 时,
时,![]() 在区间
在区间![]() 上有且仅有一个零点;
上有且仅有一个零点;
当![]() 或
或![]() 时,
时,![]() 在区间
在区间![]() 上有两个零点.
上有两个零点.

练习册系列答案
相关题目
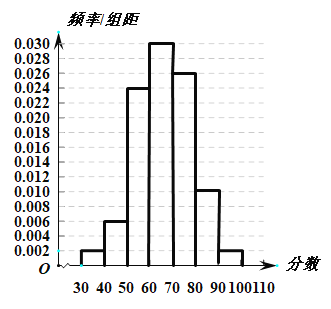
【题目】在全面建成小康社会的决胜阶段,让贫困地区同全国人民共同进入全面小康社会是我们党的庄严承诺.在“脱真贫、真脱贫”的过程中,精准扶贫助推社会公平显得尤其重要.若某农村地区有200户贫困户,经过一年扶贫后,对该地区的“精准扶贫”的成效检查验收.从这200户贫困户中随机抽出50户,对各户的人均年收入(单位:千元)进行调查得到如下频数表:
人均年收入 |
|
|
|
|
|
|
频数 | 2 | 3 | 10 | 20 | 10 | 5 |
若人均年收入在4000元以下的判定为贫困户,人均年收入在4000元~8000元的判定为脱贫户,人均年收入达到8000元的判定为小康户.
(1)用样本估计总体,估计该地区还有多少户没有脱贫;
(2)为了了解未脱贫的原因,从抽取的50户中用分层抽样的方法抽10户进行调研.
①贫困户、脱贫户、小康户分别抽到的人数是多少?
②从被抽到的脱贫户和小康户中各选1人做经验介绍,求小康户中人均年收入最高的一户被选到的概率.