题目内容
椭圆的对称中心在坐标原点,一个顶点为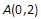 ,右焦点F与点
,右焦点F与点 的距离为2。
的距离为2。
(1)求椭圆的方程;
(2)斜率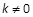 的直线
的直线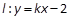 与椭圆相交于不同的两点M,N满足
与椭圆相交于不同的两点M,N满足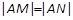 ,求直线l的方程。
,求直线l的方程。

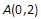 ,右焦点F与点
,右焦点F与点 的距离为2。
的距离为2。(1)求椭圆的方程;
(2)斜率
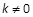 的直线
的直线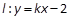 与椭圆相交于不同的两点M,N满足
与椭圆相交于不同的两点M,N满足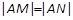 ,求直线l的方程。
,求直线l的方程。
(1)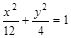 (2)
(2) 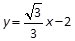 或
或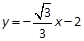
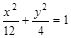 (2)
(2) 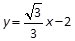 或
或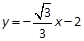
试题分析:(1)利用已知条件及椭圆中a、b、c的关系解方程组即可; (2)把线段
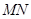 的垂直平分线与椭圆方程联立,结合判别式、利用韦达定理以及两直线垂直的充要条件即可.
的垂直平分线与椭圆方程联立,结合判别式、利用韦达定理以及两直线垂直的充要条件即可.(1)依题意,设椭圆方程为
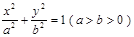 ,则其右焦点坐标为
,则其右焦点坐标为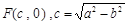 ,由
,由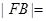
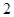 ,得
,得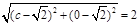 ,即
,即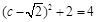 ,解得
,解得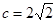 。 又 ∵
。 又 ∵ ,∴
,∴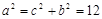 ,即椭圆方程为
,即椭圆方程为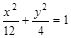 。 (4分)
。 (4分)(2)方法一:由
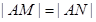 知点
知点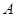 在线段
在线段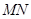 的垂直平分线上,由
的垂直平分线上,由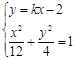 消去
消去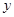 得
得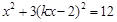 即
即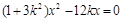 (*) ( 5分)
(*) ( 5分)由
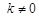 ,得方程(*)的
,得方程(*)的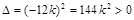 ,即方程(*)有两个不相等的实数根。 (6分)
,即方程(*)有两个不相等的实数根。 (6分)设
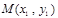 、
、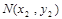 ,线段MN的中点
,线段MN的中点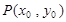 ,则
,则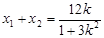 ,
,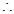
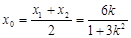 ,
,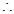
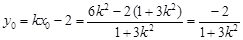 ,即
,即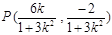
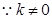 ,∴直线
,∴直线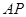 的斜率为
的斜率为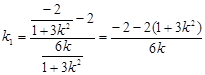 , (9分)
, (9分)由
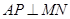 ,得
,得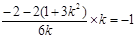 ,∴
,∴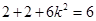 ,解得:
,解得: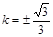 , (11分)
, (11分)∴l的方程为
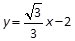 或
或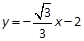 。 ( 12分)
。 ( 12分)方法二:直线l恒过点(0,-2), 且点(0,-2)在椭圆上, ∴不妨设M(0,-2), 则|AM|=4 (6分)
∴|AN|="4," 故N在以A为圆心, 4为半径的圆上,即在
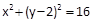 的图像上.
的图像上. 联立
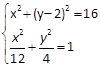 化简得
化简得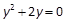 ,解得
,解得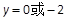 (8分)
(8分)当y=-2时,N和M重合,舍去.
当y=0时,
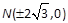 , 因此
, 因此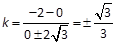 (11分)
(11分)∴l的方程为
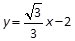 或
或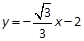 。 ( 12分)
。 ( 12分)
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
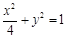 上;
上;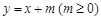 与椭圆W:
与椭圆W: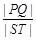 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.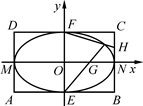
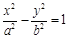 与椭圆
与椭圆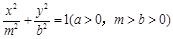 的离心率互为倒数,则( )
的离心率互为倒数,则( )



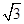 ,0),椭圆
,0),椭圆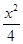 +y2=1与直线y=k(x+
+y2=1与直线y=k(x+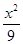 +
+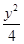 =1的交点个数是( )
=1的交点个数是( )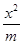 +
+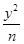 =1与双曲线
=1与双曲线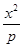 -
-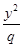 =1(m,n,p,q均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则
=1(m,n,p,q均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则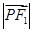 ·
·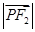 =( )
=( )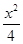 +
+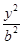 =1(b>0),直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )
=1(b>0),直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )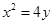 的准线与椭圆
的准线与椭圆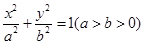 相切,且该切点与椭圆的两焦点构成的三角形面积为2,则椭圆的离心率是( )
相切,且该切点与椭圆的两焦点构成的三角形面积为2,则椭圆的离心率是( )


