题目内容
如图,已知椭圆 的焦点为F1,F2,点P为椭圆上任意一点,过F2作
的焦点为F1,F2,点P为椭圆上任意一点,过F2作 的外角平分线的垂线,垂足为点Q,过点Q作
的外角平分线的垂线,垂足为点Q,过点Q作 轴的垂线,垂足为N,线段QN的中点为M,则点M的轨迹方程为 。
轴的垂线,垂足为N,线段QN的中点为M,则点M的轨迹方程为 。
 的焦点为F1,F2,点P为椭圆上任意一点,过F2作
的焦点为F1,F2,点P为椭圆上任意一点,过F2作 的外角平分线的垂线,垂足为点Q,过点Q作
的外角平分线的垂线,垂足为点Q,过点Q作 轴的垂线,垂足为N,线段QN的中点为M,则点M的轨迹方程为 。
轴的垂线,垂足为N,线段QN的中点为M,则点M的轨迹方程为 。
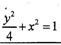
分析:点F2关于∠F1PF2的外角平分线PQ的对称点Q′在直线F1P的延长线上,故|F1Q′|=|PF1|+|PF2|=2a(椭圆长轴长),又OQ是△F2F1Q′的中位线,故|OQ|=a,由此可以求点M的轨迹方程.
解:点F2关于∠F1PF2的外角平分线PQ的对称点Q′在直线F1P的延长线上,故|F1Q′|=|PF1|+|PF2|=2a(椭圆长轴长),
又OQ是△F2F1Q′的中位线,故|OQ|=2,
设M(x,y),则Q(2x,y),
所以有4x2+y2=4,
故答案为
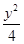 +x2=1.
+x2=1.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
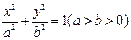 的左右焦点分别为
的左右焦点分别为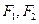 ,离心率为
,离心率为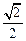 ,两焦点与上下顶点形成的菱形面积为2.
,两焦点与上下顶点形成的菱形面积为2.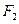 的直线
的直线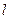 与椭圆交于A, B两点,四边形
与椭圆交于A, B两点,四边形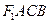 为平行四边形,
为平行四边形, 为坐标原点,且
为坐标原点,且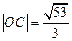 ,求直线
,求直线
 .
. 且倾斜角为
且倾斜角为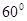 的直线交椭圆于
的直线交椭圆于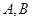 两点,若
两点,若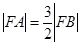 ,则椭圆的离心率等于
,则椭圆的离心率等于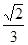
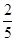
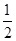
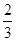
 :
: (
( )和椭圆
)和椭圆 :
: (
( )
) .给出如下四个结论:
.给出如下四个结论: ;
;  ; ④
; ④ .
.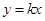 与椭圆
与椭圆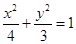 相交于
相交于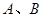 两点,分别过
两点,分别过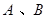 向
向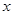 轴作垂线,若垂足恰为椭圆的两个焦点,则
轴作垂线,若垂足恰为椭圆的两个焦点,则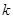 等于( ).
等于( ).

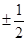

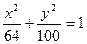 的准线方程是
的准线方程是



 ,焦点为
,焦点为 ,椭圆上的点
,椭圆上的点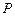 满
满 足
足 ,则
,则 的面积是
的面积是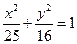 的顶点为焦点,焦点为顶点的双曲线方程,并求出其离心率.
的顶点为焦点,焦点为顶点的双曲线方程,并求出其离心率.