Question

【题目】已知矩形ABCD中，AB=2，AD=1，M为CD的中点．如图将△ADM沿AM折起，使得平面ADM⊥平面ABCM．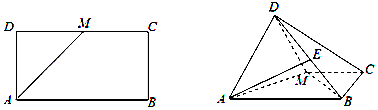

（Ⅰ）求证：BM⊥平面ADM；
（Ⅱ）若点E是线段DB上的中点，求三棱锥E﹣ABM的体积V1与四棱锥D﹣ABCM的体积V2之比．

Answer 1

【答案】证明：（Ⅰ）因为矩形ABCD中，AB=2，AD=1，M为CD的中点，

所以 ，所以AM2+BM2=AB2，所以BM⊥AM．

因为平面ADM⊥平面ABCM，平面ADM∩平面ABCM=AM，

又BM平面ABCM，且BM⊥AM，

∴BM⊥平面ADM．

（Ⅱ）因为E为DB的中点，所以 ，

又直角三角形ABM的面积 ，

梯形ABCM的面积 ，

所以 ，且 ，

所以 ．

【解析】（Ⅰ）推导出BM⊥AM，BM⊥AM，由此能证明BM⊥平面ADM．（Ⅱ）推导出 ， ，且 ，由此能求出三棱锥E﹣ABM的体积V1与四棱锥D﹣ABCM的体积V2之比．