题目内容
9.已知数列{an},若直线y=2$\sqrt{2}$x+3n(n∈N*)与圆x2+y2=an2(an>0)相切,则a2015=( )| A. | 32016 | B. | 32015 | C. | 32014 | D. | 32013 |
分析 根据直线y=2$\sqrt{2}$x+3n(n∈N*)与圆x2+y2=an2(an>0)相切,可得圆心到直线的距离d=$\frac{{3}^{n}}{\sqrt{8+1}}$=an,即可求出a2015.
解答 解:∵直线y=2$\sqrt{2}$x+3n(n∈N*)与圆x2+y2=an2(an>0)相切,
∴圆心到直线的距离d=$\frac{{3}^{n}}{\sqrt{8+1}}$=an,
∴an=3n-1,
∴a2015=32014.
故选:C.
点评 本题考查直线与圆的位置关系,考查数列知识,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
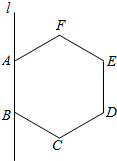 如图所示,ABCDEF是正六边形,将它绕AB所在直线l旋转,画出旋转后的几何体,并指出它是由哪几个简单几何体构成的.
如图所示,ABCDEF是正六边形,将它绕AB所在直线l旋转,画出旋转后的几何体,并指出它是由哪几个简单几何体构成的.