题目内容
函数y＝x2(x>0)的图像在点(ak，ak2)处的切线与x轴的交点的横坐标为ak＋1，其中k∈N*，若a1＝16，则a1＋a3＋a5＝________.
21
∵y′＝2x，∴k＝y′|x＝ak＝2ak，
故切线方程为y－ak2＝2ak(x－ak)，
令y＝0得x＝
ak，即ak＋1＝ak.
∴{an}是以16为首项，为公比的等比数列，
即an＝16·
n－1.
∴a1＋a3＋a5＝16＋4＋1＝21.
故切线方程为y－ak2＝2ak(x－ak)，
令y＝0得x＝
ak，即ak＋1＝ak.∴{an}是以16为首项，
为公比的等比数列，即an＝16·
n－1.∴a1＋a3＋a5＝16＋4＋1＝21.
练习册系列答案
相关题目
-1,a5=
+2a2a6+a3a7等于( )
，9S3＝S6，设Tn＝a1a2a3…an，则使Tn取最小值的n值为________．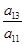
＝________.