题目内容
【题目】已知数列{an}中，a1=1，其前n项和为Sn ， 且满足an= 
（n≥2）
（1）求Sn；
（2）证明：当n≥2时，S1+ 
S2+ 
S3+…+ 
Sn＜ 
﹣ 
．
【答案】
（1）解：由an= 
（n≥2），得 
，
∴Sn﹣1﹣Sn=2SnSn﹣1，得 
，
∴数列{ 
}是以1为首项，以2为公差的等差数列，
∴ 
，
则 
（2）证明：当n≥2时， 
，
∴S1+ 
S2+ 
S3+…+ 
Sn＜ 
= 
﹣ 
【解析】（1）把已知数列递推式变形，可得数列{ }是以1为首项，以2为公差的等差数列，由此求得Sn；（2）由 ，求和后由放缩法可得S1+ S2+ S3+…+ Sn＜ ﹣ ．
【考点精析】利用数列的前n项和对题目进行判断即可得到答案，需要熟知数列{an}的前n项和sn与通项an的关系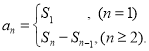
．
练习册系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
