题目内容
已知函数f(x)=ax3+bx+1(a≠0),当x=1时有极值.
(1)求a、b的关系式;
(2)若当x=1时,函数f(x)有极大值3,且经过点P(0,17)作曲线y=f(x)的切线l,求切线l的方程;
(3)设函数g(x)=f(x)-2x2(a>0)在区间(2,3)上单调递减,求a的取值范围.
(1)求a、b的关系式;
(2)若当x=1时,函数f(x)有极大值3,且经过点P(0,17)作曲线y=f(x)的切线l,求切线l的方程;
(3)设函数g(x)=f(x)-2x2(a>0)在区间(2,3)上单调递减,求a的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:计算题,导数的综合应用
分析:(1)f(x)=ax3+bx+1,f′(x)=3ax2+b,由题意可得3a+b=0;
(2)由题意得a+b+1=3,结合(1)可得a=-1,b=3,从而可得f(x)=-x3+3x+1,f′(x)=-3x2+3,设切线l与函数相切于点(m,-m3+3m+1),从而由切线方程代入即可;
(3)g(x)=f(x)-2x2=ax3-2x2-3ax+1,g′(x)=3ax2-4x-3a;化g(x)在区间(2,3)上单调递减为g′(x)>0在区间(2,3)上恒成立,从而解得.
(2)由题意得a+b+1=3,结合(1)可得a=-1,b=3,从而可得f(x)=-x3+3x+1,f′(x)=-3x2+3,设切线l与函数相切于点(m,-m3+3m+1),从而由切线方程代入即可;
(3)g(x)=f(x)-2x2=ax3-2x2-3ax+1,g′(x)=3ax2-4x-3a;化g(x)在区间(2,3)上单调递减为g′(x)>0在区间(2,3)上恒成立,从而解得.
解答:
解:(1)f(x)=ax3+bx+1,f′(x)=3ax2+b,
∵当x=1时有极值,∴3a+b=0,
即b=-3a;
(2)∵当x=1时,函数f(x)有极大值3,
∴f(1)=a+b+1=3,
又∵b=-3a,
解得,a=-1,b=3;
则f(x)=-x3+3x+1,f′(x)=-3x2+3,
设切线l与函数相切于点(m,-m3+3m+1);
故斜率k=-3m2+3;
故切线l的方程为y-(-m3+3m+1)=(-3m2+3)(x-m);
代入点P得,
17-(-m3+3m+1)=(-3m2+3)(0-m),
解得,m=2;
故切线l的方程为9x+y-17=0;
(3)g(x)=f(x)-2x2=ax3-2x2-3ax+1,
g′(x)=3ax2-4x-3a;
g(x)在区间(2,3)上单调递减可化为
g′(x)>0在区间(2,3)上恒成立,
又∵a>0,
∴
,
解得,0<a≤
.
∵当x=1时有极值,∴3a+b=0,
即b=-3a;
(2)∵当x=1时,函数f(x)有极大值3,
∴f(1)=a+b+1=3,
又∵b=-3a,
解得,a=-1,b=3;
则f(x)=-x3+3x+1,f′(x)=-3x2+3,
设切线l与函数相切于点(m,-m3+3m+1);
故斜率k=-3m2+3;
故切线l的方程为y-(-m3+3m+1)=(-3m2+3)(x-m);
代入点P得,
17-(-m3+3m+1)=(-3m2+3)(0-m),
解得,m=2;
故切线l的方程为9x+y-17=0;
(3)g(x)=f(x)-2x2=ax3-2x2-3ax+1,
g′(x)=3ax2-4x-3a;
g(x)在区间(2,3)上单调递减可化为
g′(x)>0在区间(2,3)上恒成立,
又∵a>0,
∴
|
解得,0<a≤
| 1 |
| 2 |
点评:本题考查了导数的综合应用,同时考查了恒成立问题及二次函数的最值问题等,属于难题.

练习册系列答案
相关题目
 已知A,B,C,D是函数y=sin(ωx+φ)一个周期内的图象上的四个点,如图所示,A(-
已知A,B,C,D是函数y=sin(ωx+φ)一个周期内的图象上的四个点,如图所示,A(-| π |
| 6 |
| CD |
| π |
| 12 |
A、ω=
| ||||
B、ω=
| ||||
C、ω=2,φ=
| ||||
D、ω=2,φ=
|
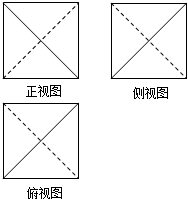 某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为( )
某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为( )A、
| ||||
| B、3π | ||||
| C、π | ||||
D、
|