题目内容
函数f(x)=ex-e2x+a,
(1)求f(x)的单调区间;
(2)若f(x)=0有两个不同解,求a的范围.
(1)求f(x)的单调区间;
(2)若f(x)=0有两个不同解,求a的范围.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:函数的性质及应用,导数的综合应用
分析:(1)对f(x)求导,令f′(x)>0,解不等式即可,
(2)由图象连续,且函数在R上先减后增,可知若函数图象与x轴两个交点,则最小值小于0即可.
(2)由图象连续,且函数在R上先减后增,可知若函数图象与x轴两个交点,则最小值小于0即可.
解答:
解:(1)f′(x)=ex-e2,
由f′(x)>0得x>2,由f′(x)<0得x<2,
∴f(x)的减区间是(-∞,2),增区间是(2,+∞),
(2)由(1)知f(x)的极小值是f(2)=a-e2,
函数在R上先减后增,图象连续,若f(x)=0有两个不同解,则f(2)<0即可
即a-e2<0,
解得a<e2.
由f′(x)>0得x>2,由f′(x)<0得x<2,
∴f(x)的减区间是(-∞,2),增区间是(2,+∞),
(2)由(1)知f(x)的极小值是f(2)=a-e2,
函数在R上先减后增,图象连续,若f(x)=0有两个不同解,则f(2)<0即可
即a-e2<0,
解得a<e2.
点评:本题考查利用导数研究函数的单调性、函数在闭区间上的最值,考查函数恒成立问题,转化为函数最值是解决恒成立问题的常用方法,导数是解决函数问题的强有力的工具.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
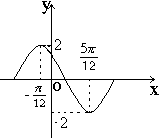 函数y=Acos(ωx+φ)在一个周期内的图象如下,此函数的解析式为( )
函数y=Acos(ωx+φ)在一个周期内的图象如下,此函数的解析式为( )A、y=2cos(2x+
| ||||
B、y=2cos(2x-
| ||||
C、y=2cos(
| ||||
D、y=2cos(2x+
|
曲线y2=|x|+1的部分图象是( )
A、 |
B、 |
C、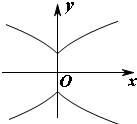 |
D、 |
不等式|x|(2x-1)≤0的解集是( )
A、(-∞,
| ||
B、(-∞,0)∪(0,
| ||
C、[-
| ||
D、[0,
|
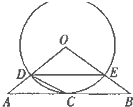 如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.
如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.