题目内容
已知函数f(x)=-3cos(
x-
)-1.
(1)求函数f(x)的周期;
(2)求函数f(x)的对称轴和对称中心;
(3)若x∈[0,π],求函数f(x)的值域.
| 1 |
| 2 |
| π |
| 4 |
(1)求函数f(x)的周期;
(2)求函数f(x)的对称轴和对称中心;
(3)若x∈[0,π],求函数f(x)的值域.
考点:三角函数的周期性及其求法,余弦函数的定义域和值域
专题:三角函数的图像与性质
分析:(1)根据函数y=Acos(ωx+φ)的周期为|
|,可得结论.
(2)根据余弦函数的对称轴和对称中心求出函数f(x)的对称轴和对称中心.
(3)若x∈[0,π],利用余弦函数的定义域和值域求得函数f(x)的值域.
| 2π |
| ω |
(2)根据余弦函数的对称轴和对称中心求出函数f(x)的对称轴和对称中心.
(3)若x∈[0,π],利用余弦函数的定义域和值域求得函数f(x)的值域.
解答:
解:(1)函数f(x)=-3cos(
x-
)-1的周期为
=2π.
(2)令
x-
=kπ,k∈z,求得x=2kπ+
,故函数的图象的对称轴为x=2kπ+
,k∈z.
令
x-
=kπ+
,k∈z,求得x=2kπ+
,故函数的图象的对称中心为 (2kπ+
,0),k∈z.
(3)若x∈[0,π],则 (
x-
)∈[-
,
],cos(
x-
)∈[
,1],故函数f(x)的值域为[-4,-
-1].
| 1 |
| 2 |
| π |
| 4 |
| 2π | ||
|
(2)令
| 1 |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
令
| 1 |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |
(3)若x∈[0,π],则 (
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| ||
| 2 |
3
| ||
| 2 |
点评:本题主要考查余弦函数的周期性、图象的对称性,余弦函数的定义域和值域,属于基础题.

练习册系列答案
相关题目
不等式|x|(2x-1)≤0的解集是( )
A、(-∞,
| ||
B、(-∞,0)∪(0,
| ||
C、[-
| ||
D、[0,
|
过抛物线y2=4x的焦点F作两条互相垂直的直线l1,l2,l1交C于A、B,l2交C于M、N.则
+
=( )
| 1 |
| |AB| |
| 1 |
| |MN| |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 截至2014年11月27目,我国机动车驾驶人数量突破3亿大关,年均增长超过两千万.为了解我地区驾驶预考人员的现状,选择A,B,C三个驾校进行调查.参加各驾校科目一预考人数如下:
截至2014年11月27目,我国机动车驾驶人数量突破3亿大关,年均增长超过两千万.为了解我地区驾驶预考人员的现状,选择A,B,C三个驾校进行调查.参加各驾校科目一预考人数如下: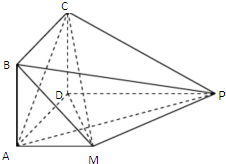 如图,四边形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD=
如图,四边形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD=