��Ŀ����
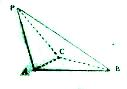
ֱ��l��y=m��mΪʵ������������E��y=|lnx|����������A��B�ĺ�����ֱ�Ϊx1��x2����x1��x2������E�ڵ�A��B��������PA��PB��y��ֱ��ڵ�M��N��������5�����ۣ�
��|
|=2��
��������PAB��������������
����ֱ��l��y��Ľ���ΪQ����|PQ|=1��
������P��ֱ��l�ľ���Ϊd����d��ȡֵ��ΧΪ��0��1����
�ݵ�x1�Ǻ���g��x��=x2+lnx�����ʱ��|
|��0Ϊ����ԭ�㣩ȡ����Сֵ��
������ȷ������ ����д��������ȷ���۵���ţ�
��|
| MN |
��������PAB��������������
����ֱ��l��y��Ľ���ΪQ����|PQ|=1��
������P��ֱ��l�ľ���Ϊd����d��ȡֵ��ΧΪ��0��1����
�ݵ�x1�Ǻ���g��x��=x2+lnx�����ʱ��|
| AO |
������ȷ������
���㣺���������ж���Ӧ��
ר�⣺������,���ν��,���������ʼ�Ӧ��,�����ĸ��Ӧ��,ֱ����Բ
����������y=m��y=|lnx|��ͼ��������ߵ�б�ʣ�������������M��N�����ɵõ�MN�ij��������жϢ٣�
ͨ��ͼ��۲�����������ߴ�ֱ�������жϢڣ����P�����꣬����PQ���������жϢܣ�
�����Ķ��壬���AO�ij������ú��������ʣ������жϢݣ�
ͨ��ͼ��۲�����������ߴ�ֱ�������жϢڣ����P�����꣬����PQ���������жϢܣ�
�����Ķ��壬���AO�ij������ú��������ʣ������жϢݣ�
���
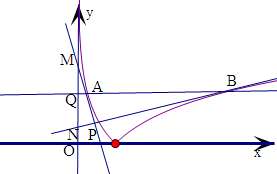 �⣺���ڢ٣���|lnx1|=|lnx2|���ɵã�
�⣺���ڢ٣���|lnx1|=|lnx2|���ɵã�
x1x2=1����0��x1��1��x2��1����A��x1��-lnx1��
B��x2��lnx2������A�㴦������б��Ϊ-
��
��B�㴦������б��Ϊ��
��
����M��0��s����N��0��n����
����
=-
����ã�s=1-lnx1��
��
=
����ã�n=lnx2-1��
����|MN|=1-lnx1-��lnx2-1��=2-ln��x1x2��=2����ٶԣ�
���ڢڣ�����PABΪ���������Σ���PA=PB����PA=AB����PB=AB��
��PA=PB����P��AB���д����ϣ������ܣ���PA=AB����P�ĺ�����С��1����������
��PB=AB��������-
•
=-1������PA��BP���������ʢڴ���
���ڢۣ�Q��0��m������y+lnx1=1-
x��y-lnx2=
-1��x1x2=1��
��ý���P��
��1-lnx1-
��������m=lnx2=-lnx1��
����|PQ|=
=1���ʢ۶ԣ�
���ڢܣ�d=m-��1-lnx1-
��=
=-1+
�ʣ�0��1�����ʢܶԣ�
���ڢݣ���x1�Ǻ���g��x��=x2+lnx�����ʱ������x12+lnx1=0��
|
|=
=
������0��x1��1����ȡ������Сֵ���ʢݴ���
�ʴ�Ϊ���٢ۢ�
 �⣺���ڢ٣���|lnx1|=|lnx2|���ɵã�
�⣺���ڢ٣���|lnx1|=|lnx2|���ɵã�x1x2=1����0��x1��1��x2��1����A��x1��-lnx1��
B��x2��lnx2������A�㴦������б��Ϊ-
| 1 |
| x1 |
��B�㴦������б��Ϊ��
| 1 |
| x2 |
����M��0��s����N��0��n����
����
| s+lnx1 |
| -x1 |
| 1 |
| x1 |
��
| n-lnx2 |
| -x2 |
| 1 |
| x2 |
����|MN|=1-lnx1-��lnx2-1��=2-ln��x1x2��=2����ٶԣ�
���ڢڣ�����PABΪ���������Σ���PA=PB����PA=AB����PB=AB��
��PA=PB����P��AB���д����ϣ������ܣ���PA=AB����P�ĺ�����С��1����������
��PB=AB��������-
| 1 |
| x1 |
| 1 |
| x2 |
���ڢۣ�Q��0��m������y+lnx1=1-
| 1 |
| x1 |
| x |
| x2 |
��ý���P��
| 2x1 |
| 1+x12 |
| 2 |
| 1+x12 |
����|PQ|=
(
|
���ڢܣ�d=m-��1-lnx1-
| 2 |
| 1+x12 |
| 1-x12 |
| 1+x12 |
| 2 |
| 1+x12 |
���ڢݣ���x1�Ǻ���g��x��=x2+lnx�����ʱ������x12+lnx1=0��
|
| AO |
| x12+(lnx1)2 |
| x14+x12 |
�ʴ�Ϊ���٢ۢ�
���������⿼�鵼���ļ������壺�����ڸõ㴦�����ߵ�б�ʣ���������ľ���͵㵽ֱ�ߵľ��빫ʽ�����麯������ֵ��������������ж������������е�����״��⣮

��ϰ��ϵ�д�
 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
�����Ŀ
����y2=|x|+1�IJ���ͼ���ǣ�������
A�� |
B�� |
C��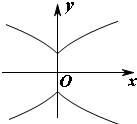 |
D�� |
����ʽ|x|��2x-1����0�Ľ⼯�ǣ�������
A����-�ޣ�
| ||
B����-�ޣ�0���ȣ�0��
| ||
C��[-
| ||
D��[0��
|