题目内容
已知A(1,0)、B(-2,0),动点M满足∠MBA=2∠MAB(∠MAB≠0).
(1)求动点M的轨迹E的方程;
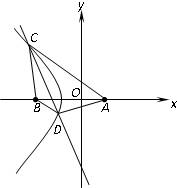
(2)若直线l:y=k(x+7),且轨迹E上存在不同的两点C、D关于直线l对称,求直线l斜率k的取值范围.
(1)求动点M的轨迹E的方程;
(2)若直线l:y=k(x+7),且轨迹E上存在不同的两点C、D关于直线l对称,求直线l斜率k的取值范围.
考点:轨迹方程,与直线关于点、直线对称的直线方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)如何体现动点M满足的条件∠MBA=2∠MAB是解决本题的关键.用动点M的坐标体现∠MBA=2∠MAB的最佳载体是直线MA、MB的斜率.
(2)先设C(x1,y1),D(x2,y2),CD的中点(x0,y0)(x1,x2,x0<-1).由点差法有y0=-3kx0.又y0=k(x0+7),考的x0=-
,y0=
k,即可求直线l斜率k的取值范围.
(2)先设C(x1,y1),D(x2,y2),CD的中点(x0,y0)(x1,x2,x0<-1).由点差法有y0=-3kx0.又y0=k(x0+7),考的x0=-
| 7 |
| 4 |
| 21 |
| 4 |
解答:
解:(1)设动点M的坐标为(x,y),则.
 由∠MBA=2∠MAB(∠MAB≠0),得
由∠MBA=2∠MAB(∠MAB≠0),得
=
,
化简得3x2-y2=3,
当∠MBA=
时也满足.
显然,动点M在线段AB的中垂线的左侧,且∠MAB≠0,
故轨迹E的方程为 3x2-y2=3(x<-1).
(2)设C(x1,y1),D(x2,y2),CD的中点(x0,y0)(x1,x2,x0<-1).
由点差法有y0=-3kx0.
又y0=k(x0+7),∴x0=-
,y0=
k,由3×(-
)2-(
k)2>3,得-
<k<
又当直线CD过点(-1,0)时,k=±
故k的取值范围是-
<k<
且k≠±
.
 由∠MBA=2∠MAB(∠MAB≠0),得
由∠MBA=2∠MAB(∠MAB≠0),得| |y| |
| x+2 |
2×
| ||
1-(
|
化简得3x2-y2=3,
当∠MBA=
| π |
| 2 |
显然,动点M在线段AB的中垂线的左侧,且∠MAB≠0,
故轨迹E的方程为 3x2-y2=3(x<-1).
(2)设C(x1,y1),D(x2,y2),CD的中点(x0,y0)(x1,x2,x0<-1).
由点差法有y0=-3kx0.
又y0=k(x0+7),∴x0=-
| 7 |
| 4 |
| 21 |
| 4 |
| 7 |
| 4 |
| 21 |
| 4 |
| ||
| 7 |
| ||
| 7 |
又当直线CD过点(-1,0)时,k=±
| ||
| 7 |
故k的取值范围是-
| ||
| 7 |
| ||
| 7 |
| ||
| 7 |
点评:求曲线的轨迹方程常采用的方法有直接法、定义法、代入法、参数法,本题主要用直接法,直接法是将动点满足的几何条件或者等量关系,直接坐标化,列出等式化简即得动点轨迹方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知△ABC中,AB=6,BC=4,∠B=60°,则△ABC的面积为( )
| A、6 | ||
| B、9 | ||
C、6
| ||
D、9
|
已知sin(
+α)=
,则cosα的值是( )
| π |
| 2 |
| 3 |
| 5 |
A、-
| ||
B、±
| ||
C、
| ||
D、
|
y=x2-3x+2在∈[
,3]上的最小值与最大值分别为( )
| 1 |
| 2 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
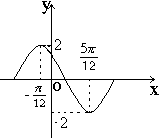 函数y=Acos(ωx+φ)在一个周期内的图象如下,此函数的解析式为( )
函数y=Acos(ωx+φ)在一个周期内的图象如下,此函数的解析式为( )A、y=2cos(2x+
| ||||
B、y=2cos(2x-
| ||||
C、y=2cos(
| ||||
D、y=2cos(2x+
|