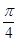题目内容
某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少75%的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区”.已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.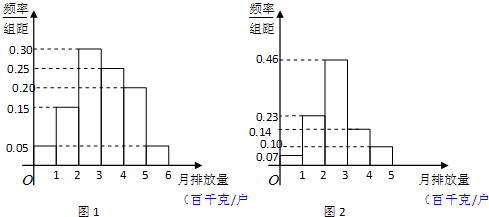
(Ⅰ)求所选的两个小区恰有一个为“非低碳小区”的概率;
(Ⅱ)假定选择的“非低碳小区”为小区A,调查显示其“低碳族”的比例为
,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区A是否达到“低碳小区”的标准?

(Ⅰ)求所选的两个小区恰有一个为“非低碳小区”的概率;
(Ⅱ)假定选择的“非低碳小区”为小区A,调查显示其“低碳族”的比例为
| 1 |
| 2 |
(Ⅰ)设三个“非低碳小区”为A,B,C,两个“低碳小区”为m,n,…(2分)
用(x,y)表示选定的两个小区,x,y∈{A,B,C,m,n},
则从5个小区中任选两个小区,所有可能的结果有10个,它们是(A,B),(A,C),(A,m),(A,n),(B,C),(B,m),(B,n),(C,m),(C,n),(m,n).…(5分)
用D表示:“选出的两个小区恰有一个为非低碳小区”这一事件,则D中的结果有6个,它们
是:(A,m),(A,n),(B,m),(B,n),(C,m),(C,n).…(7分)
故所求概率为P(D)=
=
.…(8分)
(II)由图1可知月碳排放量不超过300千克的成为“低碳族”.…(10分)
由图2可知,三个月后的低碳族的比例为0.07+0.23+0.46=0.76>0.75,…(12分)
所以三个月后小区A达到了“低碳小区”标准.…(13分)
用(x,y)表示选定的两个小区,x,y∈{A,B,C,m,n},
则从5个小区中任选两个小区,所有可能的结果有10个,它们是(A,B),(A,C),(A,m),(A,n),(B,C),(B,m),(B,n),(C,m),(C,n),(m,n).…(5分)
用D表示:“选出的两个小区恰有一个为非低碳小区”这一事件,则D中的结果有6个,它们
是:(A,m),(A,n),(B,m),(B,n),(C,m),(C,n).…(7分)
故所求概率为P(D)=
| 6 |
| 10 |
| 3 |
| 5 |
(II)由图1可知月碳排放量不超过300千克的成为“低碳族”.…(10分)
由图2可知,三个月后的低碳族的比例为0.07+0.23+0.46=0.76>0.75,…(12分)
所以三个月后小区A达到了“低碳小区”标准.…(13分)

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目


 B.
B. C.
C. D.
D.