题目内容
某校高三年级有男生105人,女生126人,教师42人,用分层抽样的方法从中抽取13人,进行问卷调查.设其中某项问题的选择支为“同意”,“不同意”两种,且每人都做了一种选择.下面表格中提供了被调查人答卷情况的部分信息.

(Ⅰ)请完成此统计表;
(Ⅱ)试估计高三年级学生“同意”的人数;
(Ⅲ)从被调查的女生中选取2人进行访谈,求选到的两名学生中,恰有一人“同意”一人“不同决的概率.”

(Ⅰ)请完成此统计表;
(Ⅱ)试估计高三年级学生“同意”的人数;
(Ⅲ)从被调查的女生中选取2人进行访谈,求选到的两名学生中,恰有一人“同意”一人“不同决的概率.”
(I)被调查人答卷情况统计表:

(II)∵由表格可以看出女生同意的概率是
,男生同意的概率是
,
用男女生同意的概率乘以人数,得到同意的结果数
×126+
×105=42+63=105(人)
(III)设“同意”的两名学生编号为1,2,
“不同意”的四名学生分别编号为3,4,5,6,
选出两人则有(1,2),(1,3),(1,4),(1,5),(1,6),
(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),
(3,6),(4,5),(4,6),(5,6)共15种方法;
其中(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),
(2,5),(2,6),8种满足题意,
则恰有一人“同意”一人“不同意”的概率为
.

(II)∵由表格可以看出女生同意的概率是
| 1 |
| 3 |
| 3 |
| 5 |
用男女生同意的概率乘以人数,得到同意的结果数
| 2 |
| 6 |
| 3 |
| 5 |
(III)设“同意”的两名学生编号为1,2,
“不同意”的四名学生分别编号为3,4,5,6,
选出两人则有(1,2),(1,3),(1,4),(1,5),(1,6),
(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),
(3,6),(4,5),(4,6),(5,6)共15种方法;
其中(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),
(2,5),(2,6),8种满足题意,
则恰有一人“同意”一人“不同意”的概率为
| 8 |
| 15 |

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
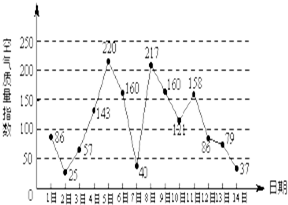
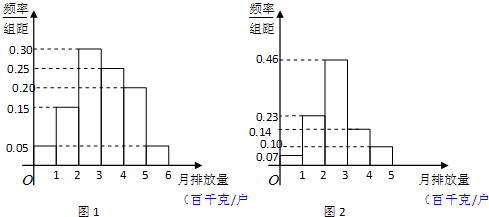

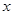 ,
,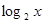 的值介于1到2之间的概率为( )
的值介于1到2之间的概率为( )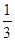

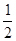

 ,从这
,从这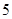 条线段中任取
条线段中任取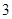 条,则所取
条,则所取
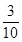
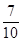
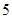 、
、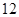 、
、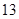 的三角形区域内随机爬行,则其到三角形顶点的距离小于
的三角形区域内随机爬行,则其到三角形顶点的距离小于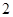 的地方的概率为 .
的地方的概率为 .