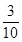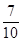题目内容
一个盒子里有2个白球、3个黄球、4个黑球.现从这个盒子里摸球,摸一个白球得3分,摸一个黄球得2分,摸一个黑球得1分.
(1)若一次摸三个球,得6分有多少种不同的摸法?
(2)若一次摸一个球,摸后不放回,求连摸3次得6分的概率;
(3)若一次摸一个球,摸后不放回,求连摸3次得分高于6分的概率.
(1)若一次摸三个球,得6分有多少种不同的摸法?
(2)若一次摸一个球,摸后不放回,求连摸3次得6分的概率;
(3)若一次摸一个球,摸后不放回,求连摸3次得分高于6分的概率.
(1)由题意可得一次摸三个球,得6分共2类不同的摸法,
即①3个黄球;②白黄黑球各1个,
故共有方法:1+2×3×4=25;
(2)共7类不同的摸法,3次摸得的球可以是:①黄黄黄②黑黄白③黑白黄④白黑黄⑤白黄黑⑥黄黑白⑦黄白黑.
故连摸3次得6分包含的基本事件数为3×2×1+2×3×4×6=150,
由计数原理可得基本事件总数为:9×8×7=504,
∴所求的概率为:
=
(3)共可分3类:①2白1黄,包含的基本事件数为:2×1×3×3=18;
②1白2黄,包含的基本事件数为:2×3×2×3=36;
③2白1黑,包含的基本事件数为:2×1×4×3=24;
∴所求事件的概率为:
=
即①3个黄球;②白黄黑球各1个,
故共有方法:1+2×3×4=25;
(2)共7类不同的摸法,3次摸得的球可以是:①黄黄黄②黑黄白③黑白黄④白黑黄⑤白黄黑⑥黄黑白⑦黄白黑.
故连摸3次得6分包含的基本事件数为3×2×1+2×3×4×6=150,
由计数原理可得基本事件总数为:9×8×7=504,
∴所求的概率为:
| 150 |
| 504 |
| 25 |
| 84 |
(3)共可分3类:①2白1黄,包含的基本事件数为:2×1×3×3=18;
②1白2黄,包含的基本事件数为:2×3×2×3=36;
③2白1黑,包含的基本事件数为:2×1×4×3=24;
∴所求事件的概率为:
| 18+36+24 |
| 504 |
| 13 |
| 84 |

练习册系列答案
相关题目
 ,从这
,从这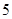 条线段中任取
条线段中任取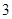 条,则所取
条,则所取