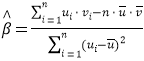题目内容
【题目】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度后,再将所得的图象向下平移一个单位长度得到函数
个单位长度后,再将所得的图象向下平移一个单位长度得到函数![]() 的图象,且
的图象,且![]() 的图象与直线
的图象与直线![]() 相邻两个交点的距离为
相邻两个交点的距离为![]() ,若
,若![]() 对任意
对任意![]() 恒成立,则
恒成立,则![]() 的取值范围是 ( )
的取值范围是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
由已知求得g(x)=2sin(ωx+![]() )﹣1,再由已知得函数g(x)的最小正周期为π,求得ω=2,结合g(x)>﹣1对任意
)﹣1,再由已知得函数g(x)的最小正周期为π,求得ω=2,结合g(x)>﹣1对任意![]() 恒成立列关于
恒成立列关于![]() 的不等式组求解.
的不等式组求解.
将函数y=2sinωx(ω>0)的图象向左平移![]() 个单位长度后,
个单位长度后,
再将所得的图象向下平移一个单位长度,
得g(x)=2sinω(x+![]() )﹣1=2sin(ωx+φ)﹣1,
)﹣1=2sin(ωx+φ)﹣1,
又y=g(x)的图象与直线y=1相邻两个交点的距离为π,得T=π,即![]() .
.
∴g(x)=2sin(2x+φ)﹣1,
当![]() 时,
时,![]() ,
,
∵![]() ,
,
∴ ,解得
,解得![]() .
.
∴φ的取值范围是![]() .
.
故选:B.

 阶梯计算系列答案
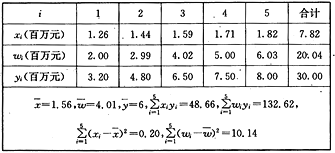
阶梯计算系列答案【题目】下表为2015年至2018年某百货零售企业的年销售额![]() (单位:万元)与年份代码
(单位:万元)与年份代码![]() 的对应关系,其中年份代码
的对应关系,其中年份代码![]() 年份-2014(如:
年份-2014(如:![]() 代表年份为2015年)。
代表年份为2015年)。
年份代码 | 1 | 2 | 3 | 4 |
年销售额 | 105 | 155 | 240 | 300 |
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测2019年该百货零售企业的年销售额;
的线性回归方程,并预测2019年该百货零售企业的年销售额;
(2)2019年,美国为遏制我国的发展,又祭出“长臂管辖”的霸权行径,单方面发起对我国的贸易战,有不少人对我国经济发展前景表示担忧.此背景下,某调查平台为了解顾客对该百货零售企业的销售额能否持续增长的看法,随机调查了60为男顾客、50位女顾客,得到如下![]() 列联表:
列联表:
持乐观态度 | 持不乐观态度 | 总计 | |
男顾客 | 45 | 15 | 60 |
女顾客 | 30 | 20 | 50 |
总计 | 75 | 35 | 110 |
问:能否在犯错误的概率不超过0.05的前提下认为对该百货零售企业的年销售额持续增长所持的态度与性别有关?
参考公式及数据:回归直线方程 ,
,
![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |