题目内容
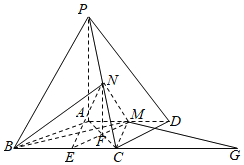
【题目】如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求四面体N-BCM的体积.
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】
(1)取BC中点E,连结EN,EM。易得四边形ABEM是平行四边形,进而平面NEM∥平面PAB,∴MN∥平面PAB.(2)设AC中点F,则VN-BCM=![]() 。求出S△BCM面积,算S△BCM面积时高时构造一个等高的△MEG ,NF=
。求出S△BCM面积,算S△BCM面积时高时构造一个等高的△MEG ,NF=![]() PA=2,带入即可。
PA=2,带入即可。
(Ⅰ)取BC中点E,连结EN,EM,∵N为PC的中点,∴NE是△PBC的中位线
∴NE∥PB,又∵AD∥BC,∴BE∥AD,
∵AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,
∴BE=![]() BC=AM=2,∴四边形ABEM是平行四边形,
BC=AM=2,∴四边形ABEM是平行四边形,
∴EM∥AB,∴平面NEM∥平面PAB,∵MN平面NEM,∴MN∥平面PAB.
(Ⅱ)取AC中点F,连结NF,∵NF是△PAC的中位线,∴NF∥PA,NF=![]() PA=2,
PA=2,
又∵PA⊥面ABCD,∴NF⊥面ABCD,如图,延长BC至G,使得CG=AM,连结GM,
∵AM![]() CG,∴四边形AGCM是平行四边形,∴AC=MG=3,
CG,∴四边形AGCM是平行四边形,∴AC=MG=3,
又∵ME=3,EC=CG=2,∴△MEG的高h=![]() ,
,
∴S△BCM=![]() ×BC×h=
×BC×h=![]() ×4×
×4×![]() =2
=2![]() ,
,
∴四面体N-BCM的体积VN-BCM=![]() .
.

【题目】某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意 | 不满意 | |
男顾客 | 40 | 10 |
女顾客 | 30 | 20 |
(1)分别估计男、女顾客对该商场服务满意的概率;
(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?
附:![]() .
.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |