题目内容
(本小题满分12分)
如图,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,平面PAD⊥平面ABCD,E、F分别为PC和BD的中点.
(1)证明:EF∥平面PAD;
(2)证明:平面PDC⊥平面PAD.
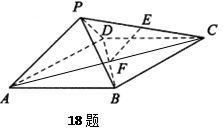
如图,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,平面PAD⊥平面ABCD,E、F分别为PC和BD的中点.
(1)证明:EF∥平面PAD;
(2)证明:平面PDC⊥平面PAD.

证明(1)连接AC
∵ABCD为矩形,F为BD的中点
∴F为AC的中点
又∵E为PC的中点,
∴EF∥AP
又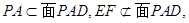
∴EF∥平面PAD.
(2)∵ABCD为矩形
∴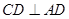
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD
∴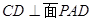
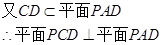
∵ABCD为矩形,F为BD的中点
∴F为AC的中点
又∵E为PC的中点,
∴EF∥AP
又
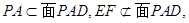
∴EF∥平面PAD.
(2)∵ABCD为矩形
∴
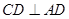
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD
∴
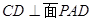
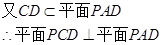
略

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
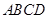 中,
中,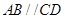 ,
,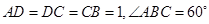 ,四边形
,四边形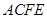 为矩形,平面
为矩形,平面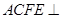 平面
平面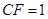 .
.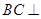 平面
平面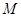 在线段
在线段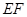 上运动,设平面
上运动,设平面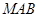 与平面
与平面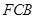 所成二面角的平面角为
所成二面角的平面角为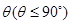 ,试求
,试求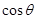 的取值范围.
的取值范围.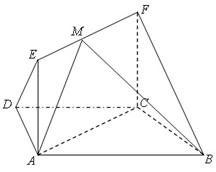
 的各棱长都是4,
的各棱长都是4, 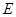 是
是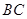 的中点,动点
的中点,动点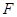 在侧棱
在侧棱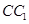 上,且不与点
上,且不与点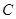 重合.
重合.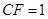 时,求证:
时,求证: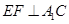 ;
;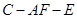 的大小为
的大小为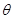 ,求
,求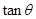 的最小值.
的最小值.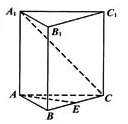
 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, 分别是
分别是 的中点,DE⊥面CBB1.
的中点,DE⊥面CBB1.  与圆柱
与圆柱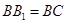 ,求
,求 与面
与面 所成角的正弦值.
所成角的正弦值.

 是以
是以 为周期的奇函数,
为周期的奇函数, ,且
,且 ,则
,则 _____________.
_____________.  ,
, ,…,
,…, ,…(
,…( 且
且 )的圆柱自下而上组成.其中每一个圆柱的高与其底面圆的
)的圆柱自下而上组成.其中每一个圆柱的高与其底面圆的 直径相等,且对于任意两个相邻圆柱,上面圆柱的高是下面圆柱的高的一半.若编号1的圆柱的高为
直径相等,且对于任意两个相邻圆柱,上面圆柱的高是下面圆柱的高的一半.若编号1的圆柱的高为 ,则所有圆柱的体
,则所有圆柱的体 积的和为_______________(结果保留
积的和为_______________(结果保留 ).
).
 已知直线
已知直线 ,给出下列命题:
,给出下列命题: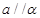 且
且 ,则
,则
 ; ②若
; ②若 ;
; ; ④若
; ④若
