题目内容
(本小题满分12分)
如图,在三棱锥ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,O为AC中点。
(1)求直线A1C与平面A1AB所成角的正弦值;
(2)在BC1上是否存在一点E,使得OE∥平面A1AB,若不存在,说明理由;若存在,确定点E的位置.

如图,在三棱锥ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,O为AC中点。
(1)求直线A1C与平面A1AB所成角的正弦值;
(2)在BC1上是否存在一点E,使得OE∥平面A1AB,若不存在,说明理由;若存在,确定点E的位置.

解:如图,因为
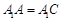 ,且O为AC的中点,所以
,且O为AC的中点,所以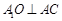 平面
平面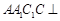 平面
平面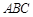 ,交线为
,交线为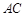 ,且
,且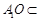 平面
平面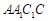 ,所以
,所以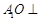 平面
平面 .……………………………1分
.……………………………1分以O为原点,
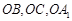 所在直线分别为x,y,z轴建立空间直角坐标系.由题意可知,
所在直线分别为x,y,z轴建立空间直角坐标系.由题意可知,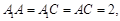 又
又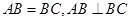
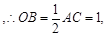
所以得:
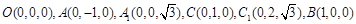 ……………………3分
……………………3分则有:
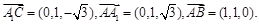 ……………4分
……………4分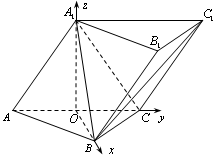
设平面
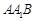 的一个法向量为
的一个法向量为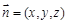 ,则有
,则有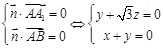 ,
,令
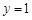 ,得
,得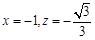
所以
 .…………………………5分
.…………………………5分 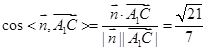
因为直线
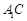 与平面
与平面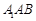 所成角
所成角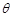 和向量
和向量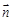 与
与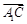 所成锐角互余,
所成锐角互余,所以
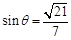 . …………………………………………………………………………6分
. …………………………………………………………………………6分(2)设
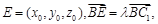
即
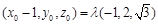 ,得
,得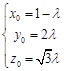 ……………………………………………8分
……………………………………………8分所以
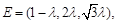 得
得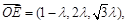 …………………………………………10分
…………………………………………10分令
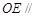 平面
平面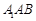 ,得
,得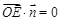 ,
,即
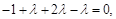 得
得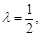 即存在这样的点E,E为
即存在这样的点E,E为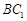 的中点. ………………12分
的中点. ………………12分略

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
 、
、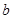 是两条不同直线,
是两条不同直线,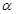 、
、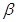 是两个不同平面,则下列四个命题:
是两个不同平面,则下列四个命题: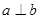 ,
,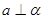 ,
,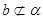 ,则
,则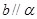 ;
;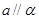 ,
,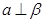 ,则
,则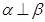 ;
;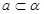 ;
;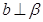 ,则
,则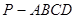 中,底面
中,底面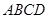 是矩形.已知
是矩形.已知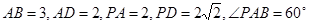 .
.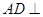 平面
平面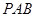 ;
;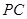 与
与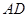 所成的角的大小;
所成的角的大小;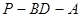 的大小.
的大小.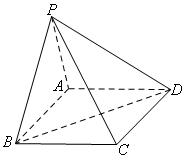
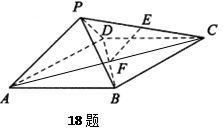
 沿对角线
沿对角线 折成直二面角后,有下列四个结论:
折成直二面角后,有下列四个结论: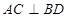 (2)
(2)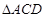 是等边三角形
是等边三角形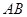 与平面
与平面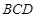 的夹角成60° (4)
的夹角成60° (4) 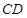 所成的角为60°
所成的角为60°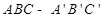 的正(主)视图和侧(左)视图如图所示. 设
的正(主)视图和侧(左)视图如图所示. 设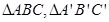 的中心分别是
的中心分别是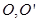 ,现将此三棱柱绕直线
,现将此三棱柱绕直线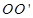 旋转,射线
旋转,射线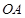 旋转所成的角为
旋转所成的角为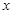 弧度(
弧度(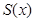 ,则函数
,则函数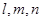 为两两不重合的直线,
为两两不重合的直线,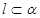 ,则
,则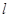 ∥
∥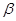
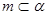 ,
,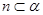 ,
,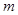 ∥β,
∥β,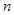 ∥β,则α∥β;
∥β,则α∥β;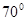 ,则∠B= ___________;
,则∠B= ___________;