题目内容
已知定义在R上的函数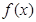 和数列
和数列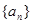 满足下列条件:
满足下列条件: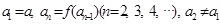 ,
,
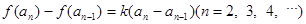 ,其中a为常数,k为非零常数.
,其中a为常数,k为非零常数.
(Ⅰ)令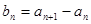
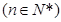 ,证明数列
,证明数列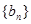 是等比数列;
是等比数列;
(Ⅱ)求数列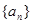 的通项公式;
的通项公式;
(Ⅲ)当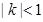 时,求
时,求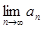 .
.
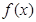 和数列
和数列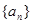 满足下列条件:
满足下列条件: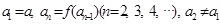 ,
,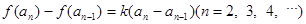 ,其中a为常数,k为非零常数.
,其中a为常数,k为非零常数.(Ⅰ)令
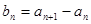
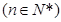 ,证明数列
,证明数列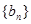 是等比数列;
是等比数列;(Ⅱ)求数列
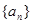 的通项公式;
的通项公式;(Ⅲ)当
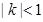 时,求
时,求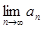 .
.(Ⅰ)证明:见解析;
(Ⅱ)数列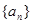 的通项公式为
的通项公式为
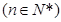 ,
,
(Ⅲ)当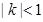 时,
时, 
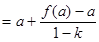
(Ⅱ)数列
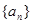 的通项公式为
的通项公式为
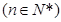 ,
,(Ⅲ)当
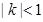 时,
时, 
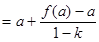
本题考查数列的性质和应用,解题时要认真审题,仔细解答.
(1)由题意知an=f(an-1),f(an)-f(an-1)=k(an-an-1)(n=2,3,4,),得an+1-an=f(an)-f(an-1)=k(an-an-1)(n=2,3,4,),由此可知an-an-1=k(an-an-1),(n=2,3,4,),得k=1.
(2)由b1=a2-a1≠0,知b2=a3-a2=f(a2)-f(a1)=k(a2-a1)≠0.因此bn=an+1-an=f(an)-f(an-1)=k(an-an-1)═kn-1(a2-a1)≠0,由此可知数列{bn}是一个公比为k的等比数列.
(3){an}是等比数列的充要条件是f(x)=kx(k≠1);先进行充分性证明:若f(x)=kx(k≠1),则{an}是等比数列.再进行必要性证明:若{an}是等比数列,f(x)=kx(k≠1).
(Ⅰ)证明:由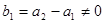 ,可得
,可得
 .由数学归纳法可证
.由数学归纳法可证
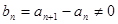
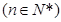 .
.
由题设条件,当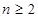 时
时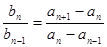
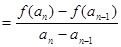

因此,数列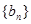 是一个公比为k的等比数列.
是一个公比为k的等比数列.
(Ⅱ)解:由(1)知,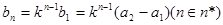
当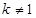 时,
时,
当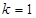 时,
时,
 .
.
而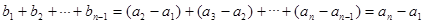

所以,当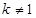 时,
时, 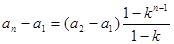
 .上式对
.上式对 也成立. 所以,数列
也成立. 所以,数列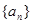 的通项公式为
的通项公式为 . 当
. 当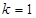 时
时
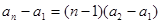
 。上式对
。上式对 也成立,所以,数列
也成立,所以,数列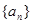 的通项公式为
的通项公式为
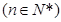 ,
,
(Ⅲ)解:当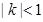 时,
时, 
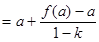
(1)由题意知an=f(an-1),f(an)-f(an-1)=k(an-an-1)(n=2,3,4,),得an+1-an=f(an)-f(an-1)=k(an-an-1)(n=2,3,4,),由此可知an-an-1=k(an-an-1),(n=2,3,4,),得k=1.
(2)由b1=a2-a1≠0,知b2=a3-a2=f(a2)-f(a1)=k(a2-a1)≠0.因此bn=an+1-an=f(an)-f(an-1)=k(an-an-1)═kn-1(a2-a1)≠0,由此可知数列{bn}是一个公比为k的等比数列.
(3){an}是等比数列的充要条件是f(x)=kx(k≠1);先进行充分性证明:若f(x)=kx(k≠1),则{an}是等比数列.再进行必要性证明:若{an}是等比数列,f(x)=kx(k≠1).
(Ⅰ)证明:由
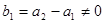 ,可得
,可得 .由数学归纳法可证
.由数学归纳法可证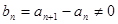
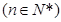 .
.由题设条件,当
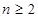 时
时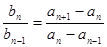
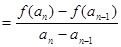

因此,数列
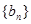 是一个公比为k的等比数列.
是一个公比为k的等比数列.(Ⅱ)解:由(1)知,
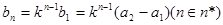
当
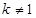 时,
时,
当
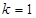 时,
时,
 .
.而
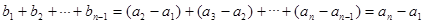

所以,当
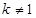 时,
时, 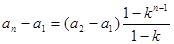
 .上式对
.上式对 也成立. 所以,数列
也成立. 所以,数列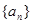 的通项公式为
的通项公式为 . 当
. 当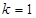 时
时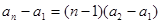
 。上式对
。上式对 也成立,所以,数列
也成立,所以,数列 的通项公式为
的通项公式为
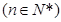 ,
,(Ⅲ)解:当
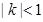 时,
时, 

练习册系列答案
相关题目
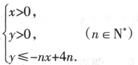 表示的平面区域为
表示的平面区域为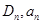 表示区域Dn中整点的个数(其中整点是指横、纵坐标都是整数的点),则
表示区域Dn中整点的个数(其中整点是指横、纵坐标都是整数的点),则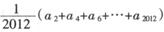 =( )
=( )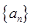 的通项公式是
的通项公式是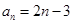 ,将数列中各项进行如下分组:第1组1个数(
,将数列中各项进行如下分组:第1组1个数(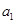 ),第2 组2个数(
),第2 组2个数(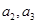 )第3组3个数(
)第3组3个数(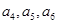 ),依次类推,……,则第16组的第10个数是 __________________.
),依次类推,……,则第16组的第10个数是 __________________.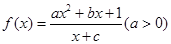 为奇函数,且
为奇函数,且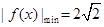 ,数列
,数列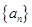 与
与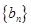 满足如下关系:
满足如下关系: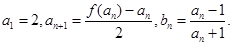
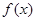 的解析式;
的解析式;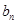 ;
;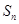 为数列
为数列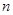 项和,求证:对任意的
项和,求证:对任意的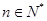 有
有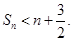
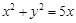 内,过点
内,过点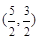 有
有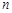 条弦的长度成等差数列,最短弦长为数列的首项
条弦的长度成等差数列,最短弦长为数列的首项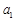 ,最长弦为
,最长弦为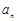 ,若公差
,若公差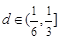 ,则
,则 .
.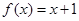 ,设
,设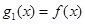 ,
,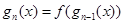
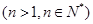 .
. 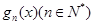 的表达式;此时若设
的表达式;此时若设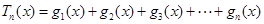 ,且关于
,且关于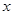 的函数
的函数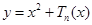
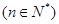 在区间
在区间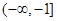 上的最小值为
上的最小值为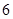 ,则求
,则求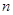 的值;
的值;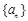 为等比数列,数列
为等比数列,数列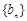 满足
满足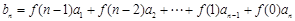 ,
,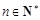 ,若
,若 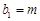 ,
,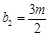 ,其中
,其中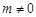 ,则
,则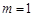 时,求
时,求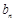 ;
;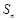 为数列
为数列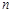 项和,若对于任意的正整数
项和,若对于任意的正整数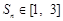 ,求实数
,求实数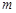 的取值范围.
的取值范围. 的公差
的公差 ,且
,且 成等比数列,则
成等比数列,则 的值是
的值是 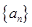 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,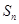 为
为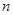 项和.
项和.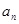 及
及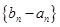 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列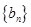 的通项公式及其前
的通项公式及其前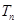 .
.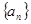 中,若
中,若 ,则
,则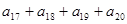 的值为( )
的值为( )


