题目内容
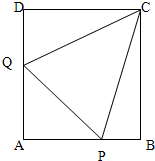已知正方形ABCD的边长为1，P、Q分别为边AB、DA上的点．设∠BCP=α，∠DCQ=β，若△APQ的周长为2，则α+β=（ ）分析：延长AB，作BE=DQ，连接CE，则△CDQ≌△CBE，再证明△QCP≌△ECP，即可得到结论．
解答：
解：延长AB，作BE=DQ，连接CE，则△CDQ≌△CBE
∴∠DCQ=∠BCE，DQ=BE，CQ=CE
∴∠QCE=∠BCE+∠BCQ=∠DCQ+∠BCQ=90°
设DQ=x，BP=y，则AQ=a-x，AP=a-y，PE=DQ+PB=x+y，
PQ=△APQ周长-AQ-AP=2a-（a-x）-（a-y）=x+y
∴△QCP≌△ECP （SSS）
∴∠QCP=∠PCE，
∴∠QCP=
=45°
∴α+β=45°
故选；C．
解：延长AB，作BE=DQ，连接CE，则△CDQ≌△CBE ∴∠DCQ=∠BCE，DQ=BE，CQ=CE
∴∠QCE=∠BCE+∠BCQ=∠DCQ+∠BCQ=90°
设DQ=x，BP=y，则AQ=a-x，AP=a-y，PE=DQ+PB=x+y，
PQ=△APQ周长-AQ-AP=2a-（a-x）-（a-y）=x+y
∴△QCP≌△ECP （SSS）
∴∠QCP=∠PCE，
∴∠QCP=
| 90° |
| 2 |
∴α+β=45°
故选；C．
点评：本题考查三角形的全等，考查学生分析问题的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知正方形ABCD的边长为2，中心为O，四边形PACE是直角梯形，设PA⊥平面ABCD，且PA=2，CE=1，
如图，已知正方形ABCD的中心为E（-1，0），一边AB所在的直线方程为x+3y-5=0，求其它三边所在的直线方程．已知正方形ABCD的边长为1，设
=
，
=
，
=
，则|
-
+
|等于（ ）
| AB |
| a |
| BC |
| b |
| AC |
| c |
| a |
| b |
| c |
| A、0 | ||
B、
| ||
| C、2 | ||
D、2
|