题目内容
(本小题满分13分)
在数列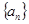 中,已知
中,已知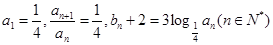 .
.
(Ⅰ)求数列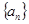 的通项公式;
的通项公式;
(Ⅱ)求证:数列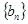 是等差数列;
是等差数列;
(Ⅲ)设数列 满足
满足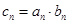 ,求
,求 的前n项和
的前n项和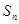 .
.
在数列
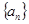 中,已知
中,已知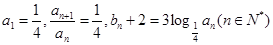 .
.(Ⅰ)求数列
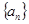 的通项公式;
的通项公式;(Ⅱ)求证:数列
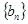 是等差数列;
是等差数列;(Ⅲ)设数列
 满足
满足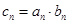 ,求
,求 的前n项和
的前n项和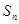 .
.(Ⅰ)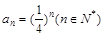 .(Ⅱ)由
.(Ⅱ)由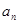 的通项公式求
的通项公式求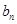 的通项公式即可得证.
的通项公式即可得证.
(Ⅲ)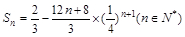
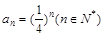 .(Ⅱ)由
.(Ⅱ)由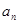 的通项公式求
的通项公式求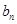 的通项公式即可得证.
的通项公式即可得证.(Ⅲ)
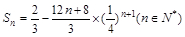
试题分析:(Ⅰ)∵
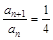
∴数列{
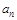 }是首项为
}是首项为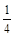 ,公比为
,公比为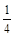 的等比数列,
的等比数列,∴
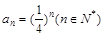 .
.(Ⅱ)∵
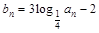
∴
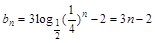 .
.∴
 ,公差d=3
,公差d=3∴数列
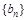 是首项
是首项 ,公差
,公差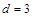 的等差数列.
的等差数列.(Ⅲ)由(Ⅰ)知,
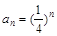 ,
,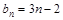 (n
(n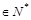 )
)∴
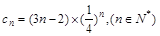 .
.∴
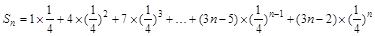 , ①
, ①于是
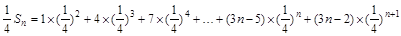 ②
②两式①-②相减得
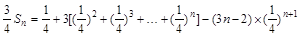
=
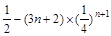 .
. ∴
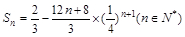 .
.点评:本题考查数列的证明,求和,着重考查数列的 “错位相减法”求和,属于中档题.

练习册系列答案
相关题目
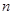 行(
行(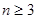 )从左向右的第3个数为 .
)从左向右的第3个数为 . 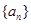 的各项均为正数,
的各项均为正数,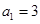 ,前
,前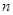 项和为
项和为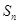 ,
,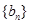 为等比数列,
为等比数列, 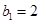 ,且
,且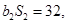
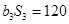 .
.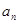 与
与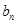 ;
;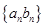 的前
的前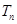 。
。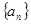 的前项
的前项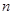 和为
和为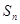 ,若
,若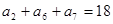 ,则
,则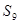 的值为( )
的值为( )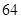
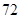
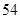
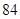
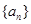 :1,4,7,……中,当
:1,4,7,……中,当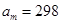 时,序号
时,序号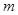 等于
等于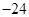 的等差数列,从第10项开始为正数,则公差
的等差数列,从第10项开始为正数,则公差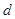 的取值范围是( )
的取值范围是( )
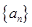 满足:
满足: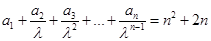 (其中常数
(其中常数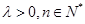 ).
).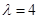 时,数列
时,数列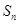 为数列
为数列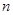 项和.求证:若任意
项和.求证:若任意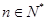 ,
,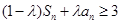
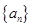 的前
的前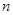 项和为
项和为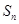 ,且满足
,且满足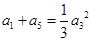 ,
,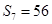 .
.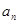 ;
;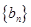 满足
满足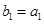 且
且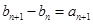 ,求数列
,求数列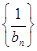 的前
的前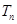 .
.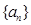 的通项公式为
的通项公式为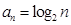 ,若其图像上存在点
,若其图像上存在点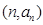 在可行域
在可行域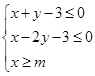 内,则
内,则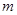 的取值范围为
的取值范围为