题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,设
,设![]() .
.
(1)若![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .①求证:数列
.①求证:数列![]() 为等差数列;②若不等式
为等差数列;②若不等式![]() 对任意的
对任意的![]() 都成立,求实数
都成立,求实数![]() 的最小值;
的最小值;
(2)若![]() ,且
,且![]() ,是否存在正整数
,是否存在正整数![]() ,使得无穷数列
,使得无穷数列![]() ,
,![]() ,
,![]() ,…成公差不为0的等差数列?若存在,给出数列
,…成公差不为0的等差数列?若存在,给出数列![]() 的一个通项公式;若不存在,请说明理由.
的一个通项公式;若不存在,请说明理由.
【答案】(1)![]() (2)不存在;详见解析
(2)不存在;详见解析
【解析】
(1)①![]() ,
,![]() ,两式相减化简得
,两式相减化简得![]() ,所以数列
,所以数列![]() 为等差数列;②先利用错位相减求出
为等差数列;②先利用错位相减求出![]() ,由不等式
,由不等式![]() 对任意的
对任意的![]() 都成立得到
都成立得到![]() 对任意
对任意![]() 恒成立,求出
恒成立,求出![]() 的最大值得解;(2)由题得当
的最大值得解;(2)由题得当![]() ,
,![]() 时
时![]() ,
,
![]() .假设存在
.假设存在![]() ,
,![]() ,
,![]() ,
,![]() ,…成等差数列,公差为
,…成等差数列,公差为![]() ,则
,则![]() ,再对
,再对![]() 分两种情况讨论得解.
分两种情况讨论得解.
(1)①因为![]() ,
,![]() ,(i)
,(i)
所以![]() .(ii)
.(ii)
将(i)![]() (ii),得
(ii),得![]() ,即
,即![]() .(iii)
.(iii)
所以,当![]() ,
,![]() 时,
时,![]() ,(iv)
,(iv)
将(iii)![]() (iv)得,
(iv)得,
当![]() ,
,![]() 时,
时,![]() ,
,
整理得,![]() ,即
,即![]() ,
,
所以数列![]() 为等差数列.
为等差数列.
②因为![]() ,令
,令![]() ,2,得
,2,得![]() ,
,![]()
解得![]() ,
,![]() ,
,
结合①可知,![]() ,故
,故![]() .
.
所以![]() ,
,
![]() ,
,
两式相减,
得![]()
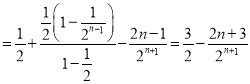 ,
,
所以![]() .
.
依题意,不等式![]() 对任意的
对任意的![]() 都成立,
都成立,
即![]() 对任意
对任意![]() 恒成立,
恒成立,
所以![]() 对任意
对任意![]() 恒成立.
恒成立.
令![]() ,
,
则![]() ,
,
所以当![]() ,2时,
,2时,![]() ,即
,即![]() ,
,
且当![]() ,
,![]() 时,
时,![]() ,即
,即![]()
所以当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,
,
所以![]() ,实数
,实数![]() 的最小值为
的最小值为![]() .
.
(2)因为![]() ,所以
,所以![]() ,即
,即![]() .
.
因为![]() ,所以
,所以![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
所以当![]() ,
,![]() 时,
时,![]() ,
,![]() .
.
假设存在![]() ,
,![]() ,
,![]() ,
,![]() ,…成等差数列,公差为
,…成等差数列,公差为![]() .
.
则![]() ,
,
(ⅰ)若![]() ,则当
,则当![]() ,
,![]() 时,
时,![]() ,
,
而![]() ,
,![]() ,所以
,所以![]() 与题意矛盾.
与题意矛盾.
(ⅱ)若![]() ,则当
,则当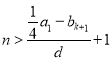 ,
,![]() 时,
时,![]() 与
与![]() 题意矛盾.
题意矛盾.
所以不存在![]() ,使得无穷数列
,使得无穷数列![]() ,
,![]() ,
,![]() ,…成公差不为0的等差数列.
,…成公差不为0的等差数列.

【题目】某市为了了解该市教师年龄分布情况,对年龄在![]() 内的5000名教师进行了抽样统计,根据分层抽样的结果,统计员制作了如下的统计表格:
内的5000名教师进行了抽样统计,根据分层抽样的结果,统计员制作了如下的统计表格:
年龄区间 |
|
|
|
|
教师人数 | 2000 | 1300 | ||
样本人数 | 130 |
由于不小心,表格中部分数据被污染,看不清了,统计员只记得年龄在![]() 的样本人数比年龄在
的样本人数比年龄在![]() 的样本人数多10,根据以上信息回答下列问题:
的样本人数多10,根据以上信息回答下列问题:

(1)求该市年龄在![]() 的教师人数;
的教师人数;
(2)试根据上表做出该市教师按照年龄的人数频率分布直方图,并求该市教师年龄的平均数![]() 及方差
及方差![]() (同一组的数据用该组区间的中点值作代表).
(同一组的数据用该组区间的中点值作代表).