题目内容
二阶矩阵A,B对应的变换对圆的区域作用结果如图所示.
(1)请写出一个满足条件的矩阵A,B;
(2)利用(1)的结果,计算C=BA,并求出曲线 在矩阵C对应的变换作用下的曲线方程.
在矩阵C对应的变换作用下的曲线方程.
(1)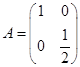 ,
,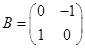 ;(2)
;(2)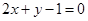
解析试题分析:(1)由图形的变化可知二阶矩阵A对应的变换是横坐标不变,纵坐标变为原来一半的变换,由此可得矩阵A.矩阵B对应的变换是逆时针旋转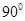 的旋转变换,由此可得矩阵B.
的旋转变换,由此可得矩阵B.
(2)由(1)的结果,可得C=BA,要求出曲线 在矩阵C对应的变换作用下的曲线方程.只需要在曲线
在矩阵C对应的变换作用下的曲线方程.只需要在曲线 上任取一点,求出该点在矩阵C作用对应的点,再代入已知的曲线方程
上任取一点,求出该点在矩阵C作用对应的点,再代入已知的曲线方程 即可得到结论.
即可得到结论.
(1)由题意,二阶矩阵A对应的变换是横坐标不变,纵坐标变为原来一半的变换,故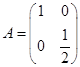
二阶矩阵B对应的变换是逆时针旋转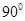 的旋转变换,故
的旋转变换,故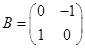 4分
4分
(2)C=BA=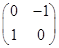
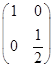 ,
,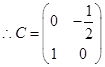
设曲线 上任意一点为
上任意一点为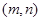 ,变换后的点坐标为
,变换后的点坐标为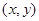
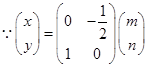 ,
,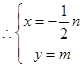 ,
,
 故所求的曲线方程为
故所求的曲线方程为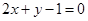 7分
7分
考点:1.图形表示矩阵的变换.2.矩阵的运算.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 -(3-2i)
-(3-2i) x-6i="0." (1)若x∈R,求x的值. (2)若x∈C,求x的值.
x-6i="0." (1)若x∈R,求x的值. (2)若x∈C,求x的值. 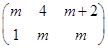 ,若该方程组无解,则实数
,若该方程组无解,则实数 的值为___________.
的值为___________.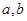 满足
满足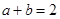 ,则行列式
,则行列式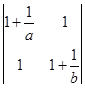 的最小值为 .
的最小值为 .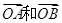 被矩阵M对应的变换
被矩阵M对应的变换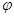 作用后分别变成
作用后分别变成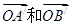 ,
,
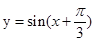 在
在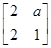 ,其中a∈R,若点P(1,-2)在矩阵M的变换下得到点P′(-4,0),求实数a的值;并求矩阵M的特征值及其对应的特征向量.
,其中a∈R,若点P(1,-2)在矩阵M的变换下得到点P′(-4,0),求实数a的值;并求矩阵M的特征值及其对应的特征向量.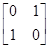 ,N=
,N= ,在平面直角坐标系中,设直线2x-y+1=0在矩阵MN对应的变换作用下得到的曲线F,求曲线F的方程.
,在平面直角坐标系中,设直线2x-y+1=0在矩阵MN对应的变换作用下得到的曲线F,求曲线F的方程. ,且以下命题都为真命题:
,且以下命题都为真命题: 实系数一元二次方程
实系数一元二次方程 的两根都是虚数;
的两根都是虚数; 存在复数
存在复数 同时满足
同时满足 且
且 .
. 的取值范围.
的取值范围.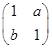 的作用下变换为曲线x2-y2=1,试求a+b的值.
的作用下变换为曲线x2-y2=1,试求a+b的值.