题目内容
【题目】用an表示自然数n的所有因数中最大的那个奇数，例如：9的因数有1，3，9，则a9=9；10的因数有1，2，5，10，则a10=5，记数列{an}的前n项和为Sn ， 则S 
= ．
【答案】
【解析】解：令an=g（n）． 由an的定义易知g（n）=g（2n），且若n为奇数则g（n）=n
令f（n）=g（1）+g（2）+g（3）+…g（2n﹣1）
则f（n+1）=g（1）+g（2）+g（3）+…g（2n+1﹣1）=1+3+…+（2n+1﹣1）+g（2）+g（4）+…+g（2n+1﹣2）
= 
2n[1+（2n+1﹣1）]+g（1）+g（2）+…+g（2n+1﹣2）=4n+f（n）
即f（n+1）﹣f（n）=4n
分别取n为1，2，…，n并累加得f（n+1）﹣f（1）=4+42+…+4n= 
= 
（4n﹣1）
又f（1）=g（1）=1，∴f（n+1）= （4n﹣1）+1．
∴S 
= ．
所以答案是： ．
【考点精析】关于本题考查的数列的前n项和，需要了解数列{an}的前n项和sn与通项an的关系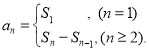
才能得出正确答案．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了解某社区居民的家庭年收入与年支出的关系，相关部门随机调查了该社区5户家庭，得到如表统计数据表：
收入x（万元） | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y（万元） | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
（1）根据上表可得回归直线方程 
= 
x+ 
，其中 =0.76， = 
﹣ 
，据此估计，该社区一户年收入为15万元的家庭年支出为多少？
（2）若从这5个家庭中随机抽选2个家庭进行访谈，求抽到家庭的年收入恰好一个不超过10万元，另一个超过11万元的概率．
