题目内容
已知函数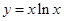 ,则这个函数在点
,则这个函数在点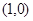 处的切线方程是( )
处的切线方程是( )
A.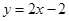 | B.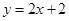 | C.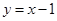 | D.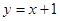 |
C
解析试题分析:∵ ,∴
,∴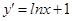 ,∴x=1时,
,∴x=1时, ,∴函数在点(1,0)处的切线方程是
,∴函数在点(1,0)处的切线方程是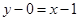 ,即
,即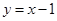 故答案为:C.
故答案为:C.
考点:导数的几何意义.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
已知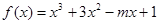 在
在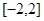 为单调增函数,则实数
为单调增函数,则实数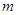 的取值范围为( )
的取值范围为( )
A.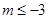 | B. | C.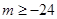 | D. |
设函数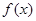 在R上存在导数
在R上存在导数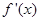 ,对任意的
,对任意的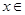 R,有
R,有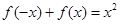 ,且
,且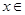 (0,+
(0,+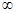 )时,
)时,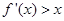 .若
.若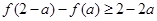 ,则实数a的取值范围为( )
,则实数a的取值范围为( )
| A.[1,+∞) | B.(-∞,1] | C.(-∞,2] | D.[2,+∞) |
曲线 与直线
与直线 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )
A. | B. | C. | D. |
设曲线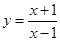 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线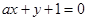 垂直,则
垂直,则 的值是
的值是
| A.2 | B.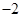 | C.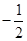 | D.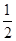 |
设函数 是
是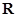 上以4为周期的可导偶函数,则曲线
上以4为周期的可导偶函数,则曲线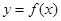 在
在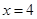 处的切线的斜率为( )
处的切线的斜率为( )
A.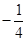 | B. | C.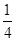 | D.4 |
定积分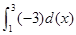 等于( )
等于( )
| A.-6 | B.6 | C.-3 | D.3 |
函数y=x2cosx的导数为( )
| A.y′=x2cosx-2xsinx | B.y′=2xcosx+x2sinx |
| C.y′=2xcosx-x2sinx | D.y′=xcosx-x2sinx |
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
| A.函数f(x)有极大值f(2)和极小值f(1) |
| B.函数f(x)有极大值f(-2)和极小值f(1) |
| C.函数f(x)有极大值f(2)和极小值f(-2) |
| D.函数f(x)有极大值f(-2)和极小值f(2) |