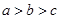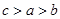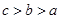题目内容
函数y=x2cosx的导数为( )
| A.y′=x2cosx-2xsinx | B.y′=2xcosx+x2sinx |
| C.y′=2xcosx-x2sinx | D.y′=xcosx-x2sinx |
C
解析试题分析:y′=(x2)′cosx+x2(cosx)′=2xcosx-x2sinx,故选C.
考点:导数的乘法与除法法则.

练习册系列答案
相关题目
已知函数 ,则这个函数在点
,则这个函数在点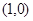 处的切线方程是( )
处的切线方程是( )
A.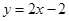 | B.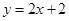 | C.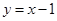 | D.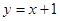 |
函数 在区间
在区间 上的最小值为( )
上的最小值为( )
A.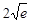 | B. | C. | D. |
若函数 在区间
在区间 上是单调函数,则实数
上是单调函数,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
观察(x2)′=2x,(x4)′=4x3,(cos x)′=-sin x,由归纳推理可得:若定义在R上的函数f(x)满足f(-x)=f(x),记g(x)为f(x)的导函数,则g(-x)等于 ( )
| A.f(x) | B.-f(x) | C.g(x) | D.-g(x) |
若f(x)=ax4+bx2+c满足f′(1)=2,则f′(﹣1)=( )
| A.﹣4 | B.﹣2 | C.2 | D.4 |
曲线y=x2和y2=x所围成的平面图形绕x轴旋转一周后,所形成的旋转体的体积为( )
A. | B. | C. | D. |
若一球的半径为r,作内接于球的圆柱,则其圆柱侧面积最大为( )
| A.2πr2 |
| B.πr2 |
| C.4πr2 |
D.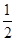 πr2 πr2 |
 的图象关于点(1,0)对称,且当
的图象关于点(1,0)对称,且当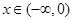 时,
时,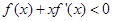 成立(其中
成立(其中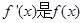 的导函数),若
的导函数),若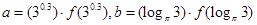 ,
,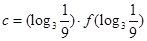 ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )