题目内容
已知函数 ,若
,若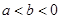 ,且
,且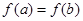 ,则
,则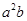 的最小值是
的最小值是
 ,若
,若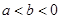 ,且
,且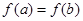 ,则
,则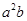 的最小值是
的最小值是 
试题分析:因为
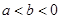 ,且
,且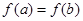 ,所以
,所以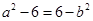 ,所以
,所以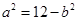 ,所以
,所以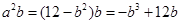 ,令
,令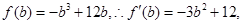 令
令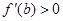 ,得
,得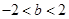 ,又因为
,又因为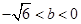 ,所以
,所以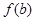 在
在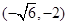 上单调递减,在
上单调递减,在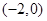 上单调递增,所以当
上单调递增,所以当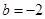 时,
时,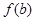 取到最小值
取到最小值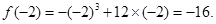
点评:解决本题的关键在于将问题转化为求
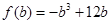 的最值,进而用导数解决.
的最值,进而用导数解决.
练习册系列答案
相关题目
题目内容
 ,若
,若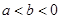 ,且
,且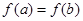 ,则
,则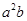 的最小值是
的最小值是 
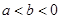 ,且
,且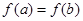 ,所以
,所以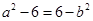 ,所以
,所以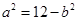 ,所以
,所以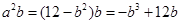 ,令
,令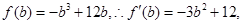 令
令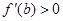 ,得
,得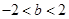 ,又因为
,又因为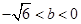 ,所以
,所以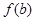 在
在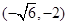 上单调递减,在
上单调递减,在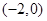 上单调递增,所以当
上单调递增,所以当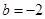 时,
时,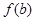 取到最小值
取到最小值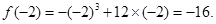
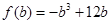 的最值,进而用导数解决.
的最值,进而用导数解决.