题目内容
(本小题满分12分)
在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x).某公司每月生产x台某种产品的收入为R(x)元,成本为C(x)元,且R(x)=3 000x-20x2,C(x)=500x+4 000(x∈N*).现已知该公司每月生产该产品不超过100台.
(1)求利润函数P(x)以及它的边际利润函数MP(x);
(2)求利润函数的最大值与边际利润函数的最大值之差.
在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x).某公司每月生产x台某种产品的收入为R(x)元,成本为C(x)元,且R(x)=3 000x-20x2,C(x)=500x+4 000(x∈N*).现已知该公司每月生产该产品不超过100台.
(1)求利润函数P(x)以及它的边际利润函数MP(x);
(2)求利润函数的最大值与边际利润函数的最大值之差.
(1)MP(x)=2 480-40x;(2)利润函数的最大值与边际利润函数的最大值之差为71 680。
试题分析:(I)由“利润等于收入与成本之差.”可求得利润函数p(x),由“边际函数为Mf(x),定义为Mf(x)=f(x+1)-f(x)”可求得边际函数;
(II)由二次函数法研究p(x)的最大值,由一次函数法研究Mp(x),对照结果即可.
(1)由题意,得x∈[1,100],且x∈N*.
P(x)=R(x)-C(x)
=(3 000x-20x2)-(500x+4 000)
=-20x2+2 500x-4 000,…………………….3分
MP(x)=P(x+1)-P(x)=[-20(x+1)2+2 500(x+1)-4 000]-(-20x2+2 500x-4 000)=2 480-40x……………………..8分
(2)P(x)=-20(x-
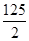 )2+74 125,
)2+74 125,当x=62或x=63时,P(x)取得最大值74 120;
因为MP(x)=2 480-40x是减函数,
所以当x=1时,MP(x)取得最大值2 440.
故利润函数的最大值与边际利润函数的最大值之差为71 680………………..12分
点评:解决该试题的关键是理解题意,将变量的实际意义符号化.同时能结合二次函数的性质得到相应的最值的求解。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
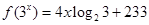 ,则
,则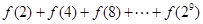 的值等于 .
的值等于 .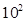 kg)与上市时间t(单位:天)的数据如下表:
kg)与上市时间t(单位:天)的数据如下表: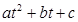 , Q= a
, Q= a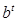 , Q=a
, Q=a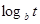 .
.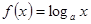 ,在
,在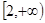 上恒有
上恒有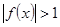 ,则实数
,则实数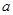 的范围是( )
的范围是( )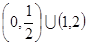
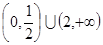


 ,若
,若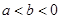 ,且
,且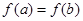 ,则
,则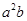 的最小值是
的最小值是  满足:
满足: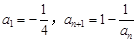 ,则
,则 =( )
=( )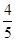
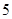


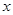 ,符号
,符号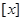 表示不超过
表示不超过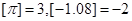 ,定义函数
,定义函数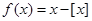 ,则下列命题中正确的是( )
,则下列命题中正确的是( )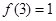
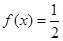 有且仅有一个解
有且仅有一个解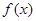 是周期函数
是周期函数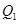 和日产量
和日产量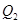 均为价格
均为价格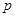 的函数,且
的函数,且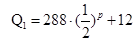
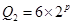 ,日成本C关于日产量
,日成本C关于日产量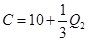
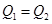 时的价格为均衡价格,求均衡价格
时的价格为均衡价格,求均衡价格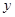 最大,求
最大,求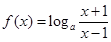 (
(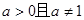 ).
).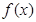 的奇偶性,并证明;
的奇偶性,并证明;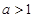 ,用单调性定义证明函数
,用单调性定义证明函数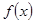 在区间
在区间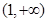 上单调递减;
上单调递减;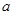 ,使得
,使得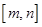 时,值域为
时,值域为 ,若存在,求出实数
,若存在,求出实数