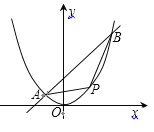
题目内容
【题目】数列
各项均不为0，前n项和为
，
，
的前n项和为
，且
（1）若数列共3项，求所有满足要求的数列；
（2）求证：
是满足已知条件的一个数列；
（3）请构造出一个满足已知条件的无穷数列，并使得
.
【答案】（1）
；
；
；（2）证明见解析；
（3）
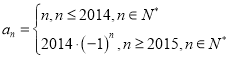
【解析】
（1）
时，
，
；
时，
，
；
时，
，
，由此能求出符合要求的数列；
（2）
，即证明
，用数学归纳法能证得结论；
（3）由已知得
，从而
，进而得到
，由此能求出结果.
（1）当时，，，解得：
或
（舍）
当时，，，即
，
解得：
或
，或
（舍）
当时，，
当时，
，解得：
或
，或
（舍），
当时，
，解得：
或（舍）
符合要求的数列有：；；
（2）
，即证明
用数学归纳法证明：
①当时，
，成立.
②假设
时，成立，即
成立
则
时，
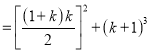
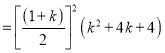
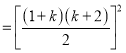
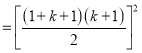
，也成立
由①②，对于
，都有
是满足已知条件的一个数列
（3）
…① 
…②
②
①得：
…③
时，
…④
③④得：
或
，
构造：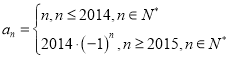
练习册系列答案
相关题目
【题目】某知名电商在
双十一购物狂欢节中成交额再创新高，
月日单日成交额达
亿元.某店主在此次购物狂欢节期间开展了促销活动，为了解买家对此次促销活动的满意情况，随机抽取了参与活动的
位买家，调查了他们的年龄层次和购物满意情况，得到年龄层次的频率分布直方图和“购物评价为满意”的年龄层次频数分布表.年龄层次的频率分布直方图：
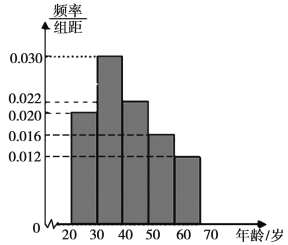
“购物评价为满意”的年龄层次频数分布表：
年龄（岁） |
|
|
|
|
|
频数 |
|
|
|
|
|
（1）估计参与此次活动的买家的平均年龄（同一组中的数据用该组区间的中点值做代表）；
（2）若年龄在
岁以下的称为“青年买家”，年龄在岁以上（含岁）的称为“中年买家”，完成下面的列联表，并判断能否有
的把握认为中、青年买家对此次活动的评价有差异？
评价满意 | 评价不满意 | 合计 | |
中年买家 | |||
青年买家 | |||
合计 |
|
附：参考公式：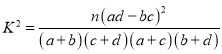
.
|
|
|
|
|
|
|
|
