题目内容
【题目】已知![]() ,函数
,函数![]() .
.
(1)若![]() ,证明:函数
,证明:函数![]() 在区间
在区间![]() 上是单调增函数;
上是单调增函数;
(2)求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(3)若函数![]() 的图像过原点,且
的图像过原点,且![]() 的导数
的导数![]() ,当
,当![]() 时,函数
时,函数![]() 过点
过点![]() 的切线至少有2条,求实数
的切线至少有2条,求实数![]() 的值.
的值.
【答案】(1)证明见解析;(2)当![]() 时,最大值为
时,最大值为![]() ;当
;当![]() 时,最大值为
时,最大值为![]() (3)
(3)![]()
【解析】
(1)由题![]() ,利用导函数求单调区间即可;
,利用导函数求单调区间即可;
(2)利用导数可以推导得到![]() 在区间
在区间![]() 上是减函数,在区间
上是减函数,在区间![]() 上是增函数,则当
上是增函数,则当![]() 时,
时,![]() 的最大值为
的最大值为![]() 和
和![]() 中的最大值,作差可得
中的最大值,作差可得![]() ,设
,设![]() ,再次利用导数推导
,再次利用导数推导![]() 的单调性,进而得到
的单调性,进而得到![]() 上的最大值;
上的最大值;
(3)由题可得![]() ,设切点为
,设切点为![]() ,则
,则![]() 处的切线方程为:
处的切线方程为:![]() ,将
,将![]() 代入可得
代入可得![]() ,则将原命题等价为关于
,则将原命题等价为关于![]() 的方程至少有2个不同的解,设
的方程至少有2个不同的解,设![]() ,进而利用导函数判断
,进而利用导函数判断![]() 的单调性,从而求解即可
的单调性,从而求解即可
(1)证明:![]() ,则
,则![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
![]()
![]() ,即此时函数
,即此时函数![]() 在区间
在区间![]() 上是单调增函数.
上是单调增函数.
(2)由(1)知,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是单调增函数,
上是单调增函数,
当![]() 时,
时,![]() ,则
,则![]() ,
,![]() ,则
,则![]() 在区间
在区间![]() 上是单调减函数;
上是单调减函数;
同理,当![]() 时,
时,![]() 在区间
在区间![]() 上是单调增函数,在区间
上是单调增函数,在区间![]() 上是单调减函数;
上是单调减函数;
即当![]() ,且
,且![]() 时,
时,![]() 在区间
在区间![]() 上是减函数,在区间
上是减函数,在区间![]() 上是增函数,
上是增函数,
则当![]() 时,
时,![]() 的最大值为
的最大值为![]() 和
和![]() 中的最大值,
中的最大值,
![]() ,
,
![]() 令
令![]() ,
,
则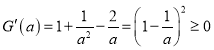 ,
,
![]()
![]() 在
在![]() 上为增函数,
上为增函数,
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ,此时最大值为
,此时最大值为![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,此时最大值为
,此时最大值为![]() .
.
(3)![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() 的图像过原点,
的图像过原点,
![]() ,即
,即![]() ,则
,则![]() ,
,
设切点为![]() ,则
,则![]() 处的切线方程为:
处的切线方程为:![]() ,
,
将![]() 代入得
代入得![]() ,
,
即![]() (※),
(※),
则原命题等价为关于![]() 的方程(※)至少有2个不同的解,
的方程(※)至少有2个不同的解,
设![]() ,
,
则![]() ,
,
令![]() ,
,![]() ,
,
![]() ,
,
当![]() 和
和![]() 时,
时,![]() ,此时函数
,此时函数![]() 为增函数;
为增函数;
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 减函数,
减函数,
![]()
![]() 的极大值为
的极大值为![]() ,
,
![]() 的极小值为
的极小值为![]() ,
,
设![]() ,则
,则![]() ,则原命题等价为
,则原命题等价为![]() ,即
,即![]() 对
对![]() 恒成立,
恒成立,
![]() 由
由![]() 得
得![]() ,
,
设![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
即![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
![]() 的最大值为
的最大值为![]() ,
,![]()
![]() ,
,
故![]() ,
,
综上所述,当![]() 时,函数
时,函数![]() 过点
过点![]() 的切线至少有2条,此时实数m的值为
的切线至少有2条,此时实数m的值为![]()

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目